Γραμμικές σχάρες σε λειτουργίες συσχέτισης ανώτερης τάξης των συστοιχιών των κβαντικών εκπομπόδων: Κατευθυντική εκτόξευση φωτονίων σε σχέση με τις αντίστοιχες οδηγίες

Τα συλλογικά φαινόμενα εκπομπής φωτός που προκύπτουν από σύνολα κβαντικών εκπομπών έχουν μεγάλη σημασία τόσο από θεμελιώδη όσο και από τεχνολογική άποψη. Από θεωρητική άποψη, τα συλλογικά αποτελέσματα δημιουργούν νέα φαινόμενα που βελτιώνουν την κατανόησή μας για τις βασικές διαδικασίες αλληλεπίδρασης φωτός-ύλης. Μερικά παραδείγματα περιλαμβάνουν superradiance [ 1 , 2 ], subradiance [ 3 , 4 ], συλλογική μετατόπιση Lamb [ 5 , 6 ], τροποποίηση των χρονικούς συσχετισμούς [ 7 , 8 ], την ενίσχυση της σύζευξης σε μία οπτική λειτουργία [ 9 ], και η αλληλεπίδραση μεταξύ ισχυρής σύζευξης και σβέσης [ 10]. Από πιο πρακτική άποψη, οι ιδιότητες εκπομπής των συνόλων των κβαντικών εκπομπών είναι σχετικές με το σχεδιασμό μη κλασικών πηγών φωτός, οι οποίες είναι γενικού ενδιαφέροντος για τις κβαντικές τεχνολογίες [ 11 , 12 , 13 ].

Πρόσφατα, παρατηρείται ολοένα και μεγαλύτερη προσοχή στην κατασκευή συστοιχιών κβαντικών εκπομπών με έλεγχο των θέσεων των επιμέρους στοιχείων τους. Συγκεκριμένα, έχουν πραγματοποιηθεί πολύ εντυπωσιακές εξελίξεις στον τομέα του οπτικού χειρισμού των ψυχρών ατόμων. Σήμερα, είναι δυνατόν να δομηθούν οριστικά μονοδιάστατες (1D) [ 14 ], δισδιάστατες (2D) [ 15 ] ή ακόμα και τρισδιάστατες (3D) [ 16 , 17 ] συστοιχίες με αρκετά αυθαίρετες γεωμετρίες και έλεγχο κάθε ατομική θέση αρκετών δεκάδων στοιχείων. Η σταθεροποίηση των θέσεων των κβαντικών εκπομπών στερεάς κατάστασης είναι πιο δύσκολη. Παρ 'όλα αυτά, υπήρξαν πολλά υποσχόμενες επιδείξεις γεωμετρίας 2D συστοιχιών που βασίζονται σε νανοπύλες διαμαντιών που περιέχουν κέντρα κενής σιλικόνης [18 ], το οπτικό γράψιμο κβαντικών στιγμών σε υδρογονωμένα κβαντικά φρεάτια [ 19 ] και ατομικά λεπτά ημιαγωγούς (ασθένεια βολφραμίουWSe2$$) που είναι τοποθετημένα πάνω από τις εικονογραφημένες επιφάνειες [ 20 ] και ακόμη και σε συνδυασμό με επιτόπιες πλασμονικές κοιλότητες [ 21 ]. Είναι πιθανό ότι οι μελλοντικές εξελίξεις θα δώσουν ακόμα πιο λεπτό έλεγχο στις ιδιότητες θέσης και εκπομπής των συστοιχιών των κβαντικών εκπομπών.

Οι διερευνήσεις φαινομένων εκπομπής που προκαλούνται από τη γεωμετρία μιας σειράς κβαντικών εκπομπών διευκολύνεται από αυτές τις προόδους κατασκευής. Με γνώμονα τις σχετικές δυνατότητες ανακαλύψεως εξωτικών φυσικών φαινομένων και υλοποίησης πρακτικών εφαρμογών μηχανικής, εισήγαμε πρόσφατα την έννοια των συστοιχιών κβαντικών κεραιών [ 22]. Αντί της συνηθισμένης εστίασης στις αλληλεπιδράσεις μεταξύ των μεμονωμένων εκπομπών, αντλήσαμε έμπνευση από τις κλασσικές συστοιχίες κεραιών και δώσαμε έμφαση στα φαινόμενα παρεμβολής που προκύπτουν από τις υπερθέσεις των πεδίων που εκπέμπονται από σύνολα κβαντικών εκπομπών. Ιδιαίτερο ενδιαφέρον οδήγησε στο γνωστό γεγονός ότι οι (κλασσικές) συστοιχίες κεραιών χρησιμοποιούν παρεμβολές για να ενισχύσουν τις ιδιότητες οδηγίας των επιμέρους στοιχείων τους με την ακτινοβολία των σύνθετων πεδίων τους σε μία ή περισσότερες επιθυμητές κατευθύνσεις [ 23 , 24 , 25 , 26]. Με έναν ανάλογο αλλά ουσιαστικά διαφορετικό τρόπο, η γεωμετρία των συστοιχιών κβαντικών κεραιών μπορεί να σχεδιαστεί για να παρέχει έλεγχο στις κατευθυντικές ιδιότητες των συσχετισμών μεταξύ των μετρημένων φωτονίων τους. Η αρχική ανάλυση στο [ 22 ] περιορίστηκε στις λειτουργίες κατευθυντικής συσχέτισης πρώτης και δεύτερης τάξης. Εδώ, επεκτείνουμε αυτό το έργο και αξιολογούμε τοΝth$$- κατεύθυνση συσχέτισης για μια σειρά Ν αρχικά διεγερμένων κβαντικών εκπομπόδων. Προηγούμενα έργα έχουν μελετήσει τοΝth$$συνάρτηση κατεύθυνσης συσχέτισης [ 27 ]. Ωστόσο, η ανάλυσή μας επικεντρώνεται στην εμφάνιση των σχιστών λοβών και πώς ο ρόλος τους επηρεάζει τα χαρακτηριστικά των συσχετίσεων φωτονίων υψηλότερης τάξης. Σημειώνουμε ότι και άλλα πρόσφατα έργα έχουν επιδιώξει έννοιες συστοιχιών κεραίας για την ανάλυση της εκπομπής από συστοιχίες κβαντικών εκπομπόρων, είτε για να διαμορφώσουν την εκπομπή ενός μόνο φωτονίου [ 28 , 29 ] είτε για να ελέγξουν συσχετισμούς δύο φωτονίων είτε σχεδιάζοντας την αρχική κατάσταση [ 30 ] ή τη συνεχή οδήγηση ενός στοιχείου και τον έλεγχο των αλληλεπιδράσεων [ 31 ].

Το υπόλοιπο του χειρόγραφου οργανώνεται ως εξής. Πρώτον, εισάγουμε το θεωρητικό πλαίσιο στο τμήμα 2 . Τότε το χρησιμοποιούμε στην ενότητα 3 για να αντλήσουμε μια εύχρηστη έκφραση για την αξιολόγηση τουΝth$$-σύνδεση κατεύθυνσης συσχέτισης. Στη συνέχεια, χρησιμοποιούμε αυτή την έκφραση στην Ενότητα 4 για να αποκαλύψουμε διαφορετικές πτυχές της δέσμης κατευθυνόμενων φωτονίων με ιδιαίτερη προσοχή στο ρόλο των λοβών σχάρας στα αντίστοιχα πρότυπα. Παρατίθενται παραδείγματα για την απεικόνιση των κύριων αποτελεσμάτων. Τέλος, τα συμπεράσματα και οι μελλοντικές προοπτικές παρουσιάζονται στο τμήμα 5 .

2. Θεωρητικό πλαίσιο

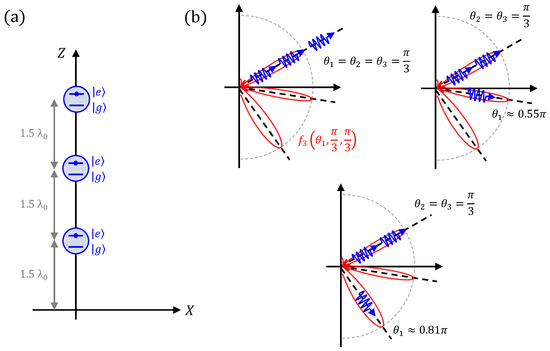
Ξεκινάμε εξετάζοντας μια γενική σειρά Ν εκπομπό που βρίσκεται σε θέσειςr1, ... , rΝ$$(βλέπε Εικόνα 1 α). Υποθέτουμε ότι όλοι οι πομποί είναι πανομοιότυποι και μπορούν να διαμορφωθούν ως συστήματα δύο επιπέδων,{ | e ⟩ , | σολ⟩ }$$, με συχνότητα γωνιακής μετάβασης ω0$$ και διπολική στιγμή p = uzΠ$$. Υποθέτουμε επίσης ότι όλοι οι εκπομποί είναι αρχικά ενθουσιασμένοι, δηλαδή, η αρχική κατάσταση του υποσυστήματος του κβαντικού εκπομπού μπορεί να γραφεί ως εξής:

| ψ ⟩ = | μι1⋯ eΝ⟩ =Πn = 1Νσˆ†n| 0 ⟩$$$$

(1)

Σχήμα 2. ( a ) Σκίτσο της γεωμετρίας. Μια γραμμική συστοιχίαΝ= 3 ομοιόμορφα κατανεμημένους κβαντικούς εκπομπούς με διανύσματα θέσης rn= n d, n = 1 , 2 , 3, και ρε= 1,5 λ0, λ0που είναι το μήκος κύματος στη συχνότητα μετάβασης τους, προσανατολίζεται κατακόρυφα κατά μήκος του άξονα Ζ. ( β ) Σχέδιο τριών αποτελεσμάτων μέτρησης με την ίδια πιθανότητα. Κορυφαία αριστερά: Μετρήθηκαν τρία φωτόνια κατά την ίδια κατεύθυνσηθ1= θ2= θ3= π/ 3. Κορυφαία δεξιά: Δύο φωτόνια μετριούνται κατά μήκος αυτής της κατεύθυνσης:θ2= θ3= π/ 3, και το υπόλοιπο φωτόνιο μετράται κατά μήκος της πρώτης κατεύθυνσης λοβού σχισμής θ1= acos ( cos π3- 2 πκ0ρε≃ 0,55 π). Κέντρο πυθμένα: Δύο φωτόνια μετριούνται κατά μήκος της κατεύθυνσηςθ2= θ3= π/ 3, και το υπόλοιπο φωτόνιο μετράται κατά μήκος της δεύτερης κατεύθυνσης λοβού σχισμής, θ1= acos ( cos π3- 4 πκ0ρε≃ 0,81 π). Για αναφορά, η κόκκινη γραμμή υποδεικνύει τοΝth-order factor factor φά3( θ1, θ2, θ3) ως συνάρτηση του θ1 και εκτιμήθηκε σε θ2= θ3= π/ 3. Για να απελευθερωθεί περισσότερο φως σε αυτό το αποτέλεσμα, το Σχήμα 3 περιλαμβάνει μία εκτεταμένη παραμετρική ανάλυση του γενικευμένου συντελεστή κβαντικής διάταξης για μια γραμμική κατακόρυφη διάταξηΝ= 3ομοιόμορφα διαχωρισμένα στοιχεία. Παρουσιάζεται γραφικά ως συνάρτηση της απόστασης διαχωρισμού των στοιχείων, d , και των κατευθύνσεων αξιολόγησης, (θ1, θ2, θ3). Όπως αναμένεται, παρατηρούνται πολύ διαφορετικές συμπεριφορές ως συνάρτηση της απόστασης χωρισμού μεταξύ των εκπομπόδων. Για ένα διαχωρισμό διηλεκτρικού μήκους,ρε= 0,1 λ0 (λ0 που είναι το μήκος κύματος στη συχνότητα μετάβασης), ο συντελεστής κβαντικής συστοιχίας μεγιστοποιείται πάντοτε στα σημεία στα οποία οι τρεις κατευθύνσεις αξιολόγησης είναι ταυτόσημες, θ1= θ2= θ3. Αυτό σημαίνει ότι τα φωτόνια τείνουν να συσσωρεύονται γύρω από την ίδια κατεύθυνση για αυτή τη σειρά υποβρύχιων γραμμών. Το εύρος δέσμης γύρω από τη μέγιστη κατεύθυνση μειώνεται καθώς αυξάνεται ο διαχωρισμός μεταξύ των εκπομπών.