Αρθρο Ανοιχτή πρόσβαση Που δημοσιεύθηκε: 30 Ιανουαρίου 2020 Παρατηρήσιμη κβαντική εμπλοκή λόγω βαρύτητας Tanjung Krisnanda ,Guo Yao Tham ,Mauro Paternostro &Tomasz Paterek npj Κβαντικός όγκοςπληροφοριών 6 , αριθμός άρθρου: 12 ( 2020 ) Αναφέρετε αυτό το άρθρο 823 Πρόσβαση 1 Αναφορές 5 Altmetric Στοιχείαμετρήσεων Αφηρημένη Κανένα πείραμα μέχρι σήμερα δεν παρείχε στοιχεία για τα κβαντικά χαρακτηριστικά της βαρυτικής αλληλεπίδρασης. Οι πρόσφατα προτεινόμενες δοκιμές προτείνουν την αναζήτηση της δημιουργίας κβαντικής εμπλοκής μεταξύ μαζικών αντικειμένων ως πιθανής οδού προς την παρατήρηση τέτοιων χαρακτηριστικών. Με γνώμονα την πρόοδο της οπτικής ψύξης των καθρεπτών, εδώ παρέχουμε μια συστηματική μελέτη της εμπλοκής μεταξύ δύο μαζών που συνδέονται με βαρύτητα. Αρχικά θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε αρμονικές δυνατότητες (οπτομηχανική) και στη συνέχεια τις μάζες που απελευθερώνονται από τις παγίδες. Αυτό οδηγεί στην εκτίμηση των πειραματικών παραμέτρων που απαιτούνται για την παρατήρηση της επαγόμενης από βαρύτητα εμπλοκής. Η οπτομηχανική εγκατάσταση απαιτεί κάτοπτρα τύπου LIGO και συμπιέσεις ή μεγάλους χρόνους συνοχής, αλλά οι απελευθερωμένες μάζες μπορεί να είναι ελαφρές και να συσσωρεύουν ανιχνεύσιμη εμπλοκή σε χρονικό διάστημα μικρότερο από τους χρόνους συνοχής τους. Δεν αναπτύσσεται μακροσκοπική κβαντική υπέρθεση κατά τη διάρκεια της εξέλιξης. Συζητάμε τις συνέπειες από τέτοια πειράματα σκέψης σχετικά με τη φύση της βαρυτικής σύζευξης. Εισαγωγή Η επιτυχής ενοποίηση των ηλεκτρομαγνητικών, αδύναμων και ισχυρών αλληλεπιδράσεων μέσα στο κβαντικό πλαίσιο υποδηλώνει έντονα ότι η βαρύτητα πρέπει επίσης να ποσοτικοποιηθεί. Ωστόσο, μέχρι σήμερα δεν υπάρχουν πειραματικές ενδείξεις για κβαντικά χαρακτηριστικά βαρύτητας. Σε πολλά πειράματα, η βαρύτητα είναι το κλειδί για την ερμηνεία των παρατηρούμενων δεδομένων, αλλά αρκεί η χρήση της Νευτώνειας θεωρίας (κβαντικό σωματίδιο που κινείται σε ένα κλασσικό πεδίο υπόβαθρου) ή γενικής σχετικότητας (κβαντικό σωματίδιο που κινείται σε σταθερό χωροχρόνο) των δεδομένων αυτών. Τα πειράματα ορόσημων που περιγράφονται στο πλαίσιο της Νευτώνειας περιλαμβάνουν μετατόπιση κβαντικής φάσης που προκαλείται από βαρύτητα σε συμβολισμό κάθετου νετρονίου, 1 ακριβής μέτρηση βαρυτικής επιτάχυνσης με πτώση ατόμων, 2ή κβαντικές καταστάσεις των νετρονίων σε ένα περιοριστικό δυναμικό που δημιουργείται από το πεδίο βαρύτητας και έναν οριζόντιο καθρέφτη. 3 Κβαντικά πειράματα που απαιτούν γενική σχετικότητα περιλαμβάνουν βαρυτική ερυθρή μετατόπιση της ηλεκτρομαγνητικής ακτινοβολίας 4 ή χρονική διαστολή ατομικών ρολογιών σε διαφορετικά ύψη. 5 Ορισμένες θεωρητικές προτάσεις συζήτησαν σενάρια ικανά να αποκαλύψουν την κβαντικότητα της βαρύτητας. Για παράδειγμα, οι αναφορές. 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 πρότειναν την παρατήρηση μιας μάζας ανιχνευτή που αλληλεπιδρά με το πεδίο βαρύτητας που δημιουργείται από μια άλλη μάζα. Πιο πρόσφατες προτάσεις βάζουν τη βαρύτητα σε ρόλο μεσολαβητή κβαντικών συσχετισμών και βασίζονται στο γεγονός ότι η κβαντική εμπλοκή μεταξύ αλλιώς μη αλληλεπιδρώντων αντικειμένων μπορεί να αυξηθεί μόνο μέσω ενός κβαντικού μεσολαβητή. 15 , 16 , 17Με τη βοήθεια αυτών των προτάσεων και από τις προόδους στην οπτομηχανική, 18 ειδικότερα η ψύξη μαζικών μηχανικών (μακροσκοπικών) ταλαντωτών πλησίον της κβαντικής κατάστασης 19 , 20 , 21 και η μέτρηση της κβαντικής εμπλοκής ενός συστήματος δύο τρόπων 22 , 23 , 24 μελετούμε δύο κοντινές ψυχρές μάζες που αλληλεπιδρούν βαρυτικά. Προτείνουμε δύο σενάρια ικανά να αυξήσουν τη βαρυτική εμπλοκή μεταξύ των μαζών. Στο πρώτο σενάριο, θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε 1D αρμονικές δυνατότητες (optomechanics). Στη δεύτερη, οι μάζες απελευθερώνονται από τις οπτικές παγίδες. Και για τις δύο ρυθμίσεις, αντλούμε ένα αναλυτικό σχήμα αξίας που χαρακτηρίζει την ποσότητα της εμπλοκής που προκαλείται από τη βαρύτητα και το χρόνο που χρειάζεται για την παρατήρηση της. Η παράδοση περιλαμβάνει διάφορες αρχικές καταστάσεις και δείχνει ότι τα αντικείμενα πρέπει να ψυχθούν πολύ κοντά στις καταστάσεις εδάφους τους και ότι η συμπίεση της αρχικής τους κατάστασης ενισχύει σημαντικά την ποσότητα της δημιουργούμενης εμπλοκής. Στη συνέχεια διατυπώνουμε μια αριθμητική προσέγγιση, η οποία εξηγεί όλες τις σχετικές πηγές θορύβου που επηρεάζουν τις ρυθμίσεις που προτείνουμε, για να προσδιορίσει ένα σύνολο παραμέτρων που απαιτούνται για την παρατήρηση τέτοιου είδους εμπλοκής. Τέλος, συζητούμε τα συμπεράσματα που μπορούν να αντληθούν από αυτό το πείραμα με έμφαση στην ανάγκη για ανεξάρτητη εργαστηριακή επαλήθευση ότι η βαρυτική αλληλεπίδραση μεταξύ των κοντινών αντικειμένων πράγματι διαμεσολαβείται. Αποτελέσματα Προτεινόμενη ρύθμιση Εξετάστε δύο σωματίδια, χωρισμένα με απόσταση L , όπως απεικονίζεται στο σχήμα 1 . Στη συνέχεια, μελετάμε τη θέση όπου τα τεράστια σωματίδια κρατούνται ή απελευθερώνονται από τις μονοδιάστατες αρμονικές παγίδες. Στην πρώτη περίπτωση, μπορούμε να επεξεργαστούμε τα σωματίδια ως πανομοιότυπους αρμονικούς ταλαντωτές, με το ίδιο σχήμα, μάζα m , και συχνότητα ω vibration . Οι δύο ταλαντωτές και η βαρυτική αλληλεπίδραση μεταξύ τους δημιουργούν το σύνολο Χαμιλτονιανή H = H 0 + H g , όπου {{} {{} {{} {{} {{} {{} {{}} { {A} ^ {2} + \ frac {{p} _ {B} ^ {2}} {2m} + \ frac {1} {2} {x} } ^ {2} $$ (1) και H ζ περιγράφει τη βαρυτική όρο. Αν οι αρμονικές παγίδες αφαιρεθούν, ο αντίστοιχος Χ Hamiltonian απλοποιείται σε \ ({H} _ {0} = ({p} _ {A} ^ {2} + {p} _ {B} ^ {2} ) . Προτού προχωρήσουμε σε λεπτομερείς υπολογισμούς, θα συζητήσουμε τα γενικά χαρακτηριστικά του βαρυτικού όρου και τις προϋποθέσεις που απαιτούνται για τη δημιουργία εμπλοκής. Εικόνα 1: Προτεινόμενη πειραματική ρύθμιση. Φιγούρα 1 Δύο μάζες, τοποθετημένες σε απόσταση L , είτε παγιδεύονται με αρμονικά δυναμικά ανά πάσα στιγμή είτε απελευθερώνονται μετά την επίτευξη της ψύξης. Τα σωματίδια υποτίθεται ότι ψύχονται κοντά στην κατάσταση εδάφους των δυνατοτήτων παγίδευσης τους. Μελετάμε την εμπλοκή που δημιουργείται και στα δύο σενάρια και σημειώστε ότι μπορεί να ερευνηθεί με αδύναμα πεδία φωτός. Το μοντέλο μας περιλαμβάνει την βαρυτική σύζευξη (κυρίαρχη), τον θόρυβο, την απόσβεση, την αποκάλυψη και τις δυνάμεις Casimir. Αρθρο Ανοιχτή πρόσβαση Που δημοσιεύθηκε: 30 Ιανουαρίου 2020 Παρατηρήσιμη κβαντική εμπλοκή λόγω βαρύτητας Tanjung Krisnanda ,Guo Yao Tham ,Mauro Paternostro &Tomasz Paterek npj Κβαντικός όγκοςπληροφοριών 6 , αριθμός άρθρου: 12 ( 2020 ) Αναφέρετε αυτό το άρθρο 823 Πρόσβαση 1 Αναφορές 5 Altmetric Στοιχείαμετρήσεων Αφηρημένη Κανένα πείραμα μέχρι σήμερα δεν παρείχε στοιχεία για τα κβαντικά χαρακτηριστικά της βαρυτικής αλληλεπίδρασης. Οι πρόσφατα προτεινόμενες δοκιμές προτείνουν την αναζήτηση της δημιουργίας κβαντικής εμπλοκής μεταξύ μαζικών αντικειμένων ως πιθανής οδού προς την παρατήρηση τέτοιων χαρακτηριστικών. Με γνώμονα την πρόοδο της οπτικής ψύξης των καθρεπτών, εδώ παρέχουμε μια συστηματική μελέτη της εμπλοκής μεταξύ δύο μαζών που συνδέονται με βαρύτητα. Αρχικά θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε αρμονικές δυνατότητες (οπτομηχανική) και στη συνέχεια τις μάζες που απελευθερώνονται από τις παγίδες. Αυτό οδηγεί στην εκτίμηση των πειραματικών παραμέτρων που απαιτούνται για την παρατήρηση της επαγόμενης από βαρύτητα εμπλοκής. Η οπτομηχανική εγκατάσταση απαιτεί κάτοπτρα τύπου LIGO και συμπιέσεις ή μεγάλους χρόνους συνοχής, αλλά οι απελευθερωμένες μάζες μπορεί να είναι ελαφρές και να συσσωρεύουν ανιχνεύσιμη εμπλοκή σε χρονικό διάστημα μικρότερο από τους χρόνους συνοχής τους. Δεν αναπτύσσεται μακροσκοπική κβαντική υπέρθεση κατά τη διάρκεια της εξέλιξης. Συζητάμε τις συνέπειες από τέτοια πειράματα σκέψης σχετικά με τη φύση της βαρυτικής σύζευξης. Εισαγωγή Η επιτυχής ενοποίηση των ηλεκτρομαγνητικών, αδύναμων και ισχυρών αλληλεπιδράσεων μέσα στο κβαντικό πλαίσιο υποδηλώνει έντονα ότι η βαρύτητα πρέπει επίσης να ποσοτικοποιηθεί. Ωστόσο, μέχρι σήμερα δεν υπάρχουν πειραματικές ενδείξεις για κβαντικά χαρακτηριστικά βαρύτητας. Σε πολλά πειράματα, η βαρύτητα είναι το κλειδί για την ερμηνεία των παρατηρούμενων δεδομένων, αλλά αρκεί η χρήση της Νευτώνειας θεωρίας (κβαντικό σωματίδιο που κινείται σε ένα κλασσικό πεδίο υπόβαθρου) ή γενικής σχετικότητας (κβαντικό σωματίδιο που κινείται σε σταθερό χωροχρόνο) των δεδομένων αυτών. Τα πειράματα ορόσημων που περιγράφονται στο πλαίσιο της Νευτώνειας περιλαμβάνουν μετατόπιση κβαντικής φάσης που προκαλείται από βαρύτητα σε συμβολισμό κάθετου νετρονίου, 1 ακριβής μέτρηση βαρυτικής επιτάχυνσης με πτώση ατόμων, 2ή κβαντικές καταστάσεις των νετρονίων σε ένα περιοριστικό δυναμικό που δημιουργείται από το πεδίο βαρύτητας και έναν οριζόντιο καθρέφτη. 3 Κβαντικά πειράματα που απαιτούν γενική σχετικότητα περιλαμβάνουν βαρυτική ερυθρή μετατόπιση της ηλεκτρομαγνητικής ακτινοβολίας 4 ή χρονική διαστολή ατομικών ρολογιών σε διαφορετικά ύψη. 5 Ορισμένες θεωρητικές προτάσεις συζήτησαν σενάρια ικανά να αποκαλύψουν την κβαντικότητα της βαρύτητας. Για παράδειγμα, οι αναφορές. 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 πρότειναν την παρατήρηση μιας μάζας ανιχνευτή που αλληλεπιδρά με το πεδίο βαρύτητας που δημιουργείται από μια άλλη μάζα. Πιο πρόσφατες προτάσεις βάζουν τη βαρύτητα σε ρόλο μεσολαβητή κβαντικών συσχετισμών και βασίζονται στο γεγονός ότι η κβαντική εμπλοκή μεταξύ αλλιώς μη αλληλεπιδρώντων αντικειμένων μπορεί να αυξηθεί μόνο μέσω ενός κβαντικού μεσολαβητή. 15 , 16 , 17Με τη βοήθεια αυτών των προτάσεων και από τις προόδους στην οπτομηχανική, 18 ειδικότερα η ψύξη μαζικών μηχανικών (μακροσκοπικών) ταλαντωτών πλησίον της κβαντικής κατάστασης 19 , 20 , 21 και η μέτρηση της κβαντικής εμπλοκής ενός συστήματος δύο τρόπων 22 , 23 , 24 μελετούμε δύο κοντινές ψυχρές μάζες που αλληλεπιδρούν βαρυτικά. Προτείνουμε δύο σενάρια ικανά να αυξήσουν τη βαρυτική εμπλοκή μεταξύ των μαζών. Στο πρώτο σενάριο, θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε 1D αρμονικές δυνατότητες (optomechanics). Στη δεύτερη, οι μάζες απελευθερώνονται από τις οπτικές παγίδες. Και για τις δύο ρυθμίσεις, αντλούμε ένα αναλυτικό σχήμα αξίας που χαρακτηρίζει την ποσότητα της εμπλοκής που προκαλείται από τη βαρύτητα και το χρόνο που χρειάζεται για την παρατήρηση της. Η παράδοση περιλαμβάνει διάφορες αρχικές καταστάσεις και δείχνει ότι τα αντικείμενα πρέπει να ψυχθούν πολύ κοντά στις καταστάσεις εδάφους τους και ότι η συμπίεση της αρχικής τους κατάστασης ενισχύει σημαντικά την ποσότητα της δημιουργούμενης εμπλοκής. Στη συνέχεια διατυπώνουμε μια αριθμητική προσέγγιση, η οποία εξηγεί όλες τις σχετικές πηγές θορύβου που επηρεάζουν τις ρυθμίσεις που προτείνουμε, για να προσδιορίσει ένα σύνολο παραμέτρων που απαιτούνται για την παρατήρηση τέτοιου είδους εμπλοκής. Τέλος, συζητούμε τα συμπεράσματα που μπορούν να αντληθούν από αυτό το πείραμα με έμφαση στην ανάγκη για ανεξάρτητη εργαστηριακή επαλήθευση ότι η βαρυτική αλληλεπίδραση μεταξύ των κοντινών αντικειμένων πράγματι διαμεσολαβείται. Αποτελέσματα Προτεινόμενη ρύθμιση Εξετάστε δύο σωματίδια, χωρισμένα με απόσταση L , όπως απεικονίζεται στο σχήμα 1 . Στη συνέχεια, μελετάμε τη θέση όπου τα τεράστια σωματίδια κρατούνται ή απελευθερώνονται από τις μονοδιάστατες αρμονικές παγίδες. Στην πρώτη περίπτωση, μπορούμε να επεξεργαστούμε τα σωματίδια ως πανομοιότυπους αρμονικούς ταλαντωτές, με το ίδιο σχήμα, μάζα m , και συχνότητα ω vibration . Οι δύο ταλαντωτές και η βαρυτική αλληλεπίδραση μεταξύ τους δημιουργούν το σύνολο Χαμιλτονιανή H = H 0 + H g , όπου {{} {{} {{} {{} {{} {{} {{}} { {A} ^ {2} + \ frac {{p} _ {B} ^ {2}} {2m} + \ frac {1} {2} {x} } ^ {2} $$ (1) και H ζ περιγράφει τη βαρυτική όρο. Αν οι αρμονικές παγίδες αφαιρεθούν, ο αντίστοιχος Χ Hamiltonian απλοποιείται σε \ ({H} _ {0} = ({p} _ {A} ^ {2} + {p} _ {B} ^ {2} ) . Προτού προχωρήσουμε σε λεπτομερείς υπολογισμούς, θα συζητήσουμε τα γενικά χαρακτηριστικά του βαρυτικού όρου και τις προϋποθέσεις που απαιτούνται για τη δημιουργία εμπλοκής. Εικόνα 1: Προτεινόμενη πειραματική ρύθμιση. Φιγούρα 1 Δύο μάζες, τοποθετημένες σε απόσταση L , είτε παγιδεύονται με αρμονικά δυναμικά ανά πάσα στιγμή είτε απελευθερώνονται μετά την επίτευξη της ψύξης. Τα σωματίδια υποτίθεται ότι ψύχονται κοντά στην κατάσταση εδάφους των δυνατοτήτων παγίδευσης τους. Μελετάμε την εμπλοκή που δημιουργείται και στα δύο σενάρια και σημειώστε ότι μπορεί να ερευνηθεί με αδύναμα πεδία φωτός. Το μοντέλο μας περιλαμβάνει την βαρυτική σύζευξη (κυρίαρχη), τον θόρυβο, την απόσβεση, την αποκάλυψη και τις δυνάμεις Casimir

Παρατηρήσιμη κβαντική εμπλοκή λόγω βαρύτητας

npj Κβαντικός πληροφοριών 6 , αριθμός άρθρου: 12 ( 2020 ) Αναφέρετε αυτό το άρθρο

823 Πρόσβαση
1 Αναφορές
5 Altmetric
Στοιχείαμετρήσεων

Αφηρημένη

Κανένα πείραμα μέχρι σήμερα δεν παρείχε στοιχεία για τα κβαντικά χαρακτηριστικά της βαρυτικής αλληλεπίδρασης. Οι πρόσφατα προτεινόμενες δοκιμές προτείνουν την αναζήτηση της δημιουργίας κβαντικής εμπλοκής μεταξύ μαζικών αντικειμένων ως πιθανής οδού προς την παρατήρηση τέτοιων χαρακτηριστικών. Με γνώμονα την πρόοδο της οπτικής ψύξης των καθρεπτών, εδώ παρέχουμε μια συστηματική μελέτη της εμπλοκής μεταξύ δύο μαζών που συνδέονται με βαρύτητα. Αρχικά θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε αρμονικές δυνατότητες (οπτομηχανική) και στη συνέχεια τις μάζες που απελευθερώνονται από τις παγίδες. Αυτό οδηγεί στην εκτίμηση των πειραματικών παραμέτρων που απαιτούνται για την παρατήρηση της επαγόμενης από βαρύτητα εμπλοκής. Η οπτομηχανική εγκατάσταση απαιτεί κάτοπτρα τύπου LIGO και συμπιέσεις ή μεγάλους χρόνους συνοχής, αλλά οι απελευθερωμένες μάζες μπορεί να είναι ελαφρές και να συσσωρεύουν ανιχνεύσιμη εμπλοκή σε χρονικό διάστημα μικρότερο από τους χρόνους συνοχής τους. Δεν αναπτύσσεται μακροσκοπική κβαντική υπέρθεση κατά τη διάρκεια της εξέλιξης. Συζητάμε τις συνέπειες από τέτοια πειράματα σκέψης σχετικά με τη φύση της βαρυτικής σύζευξης.

Εισαγωγή

Η επιτυχής ενοποίηση των ηλεκτρομαγνητικών, αδύναμων και ισχυρών αλληλεπιδράσεων μέσα στο κβαντικό πλαίσιο υποδηλώνει έντονα ότι η βαρύτητα πρέπει επίσης να ποσοτικοποιηθεί. Ωστόσο, μέχρι σήμερα δεν υπάρχουν πειραματικές ενδείξεις για κβαντικά χαρακτηριστικά βαρύτητας. Σε πολλά πειράματα, η βαρύτητα είναι το κλειδί για την ερμηνεία των παρατηρούμενων δεδομένων, αλλά αρκεί η χρήση της Νευτώνειας θεωρίας (κβαντικό σωματίδιο που κινείται σε ένα κλασσικό πεδίο υπόβαθρου) ή γενικής σχετικότητας (κβαντικό σωματίδιο που κινείται σε σταθερό χωροχρόνο) των δεδομένων αυτών. Τα πειράματα ορόσημων που περιγράφονται στο πλαίσιο της Νευτώνειας περιλαμβάνουν μετατόπιση κβαντικής φάσης που προκαλείται από βαρύτητα σε συμβολισμό κάθετου νετρονίου, 1 ακριβής μέτρηση βαρυτικής επιτάχυνσης με πτώση ατόμων, 2ή κβαντικές καταστάσεις των νετρονίων σε ένα περιοριστικό δυναμικό που δημιουργείται από το πεδίο βαρύτητας και έναν οριζόντιο καθρέφτη. 3 Κβαντικά πειράματα που απαιτούν γενική σχετικότητα περιλαμβάνουν βαρυτική ερυθρή μετατόπιση της ηλεκτρομαγνητικής ακτινοβολίας 4 ή χρονική διαστολή ατομικών ρολογιών σε διαφορετικά ύψη. 5

Ορισμένες θεωρητικές προτάσεις συζήτησαν σενάρια ικανά να αποκαλύψουν την κβαντικότητα της βαρύτητας. Για παράδειγμα, οι αναφορές. 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 πρότειναν την παρατήρηση μιας μάζας ανιχνευτή που αλληλεπιδρά με το πεδίο βαρύτητας που δημιουργείται από μια άλλη μάζα. Πιο πρόσφατες προτάσεις βάζουν τη βαρύτητα σε ρόλο μεσολαβητή κβαντικών συσχετισμών και βασίζονται στο γεγονός ότι η κβαντική εμπλοκή μεταξύ αλλιώς μη αλληλεπιδρώντων αντικειμένων μπορεί να αυξηθεί μόνο μέσω ενός κβαντικού μεσολαβητή. 15 , 16 , 17Με τη βοήθεια αυτών των προτάσεων και από τις προόδους στην οπτομηχανική, 18 ειδικότερα η ψύξη μαζικών μηχανικών (μακροσκοπικών) ταλαντωτών πλησίον της κβαντικής κατάστασης 19 , 20 , 21 και η μέτρηση της κβαντικής εμπλοκής ενός συστήματος δύο τρόπων 22 , 23 , 24 μελετούμε δύο κοντινές ψυχρές μάζες που αλληλεπιδρούν βαρυτικά.

Προτείνουμε δύο σενάρια ικανά να αυξήσουν τη βαρυτική εμπλοκή μεταξύ των μαζών. Στο πρώτο σενάριο, θεωρούμε τις μάζες παγιδευμένες ανά πάσα στιγμή σε 1D αρμονικές δυνατότητες (optomechanics). Στη δεύτερη, οι μάζες απελευθερώνονται από τις οπτικές παγίδες. Και για τις δύο ρυθμίσεις, αντλούμε ένα αναλυτικό σχήμα αξίας που χαρακτηρίζει την ποσότητα της εμπλοκής που προκαλείται από τη βαρύτητα και το χρόνο που χρειάζεται για την παρατήρηση της. Η παράδοση περιλαμβάνει διάφορες αρχικές καταστάσεις και δείχνει ότι τα αντικείμενα πρέπει να ψυχθούν πολύ κοντά στις καταστάσεις εδάφους τους και ότι η συμπίεση της αρχικής τους κατάστασης ενισχύει σημαντικά την ποσότητα της δημιουργούμενης εμπλοκής. Στη συνέχεια διατυπώνουμε μια αριθμητική προσέγγιση, η οποία εξηγεί όλες τις σχετικές πηγές θορύβου που επηρεάζουν τις ρυθμίσεις που προτείνουμε, για να προσδιορίσει ένα σύνολο παραμέτρων που απαιτούνται για την παρατήρηση τέτοιου είδους εμπλοκής. Τέλος, συζητούμε τα συμπεράσματα που μπορούν να αντληθούν από αυτό το πείραμα με έμφαση στην ανάγκη για ανεξάρτητη εργαστηριακή επαλήθευση ότι η βαρυτική αλληλεπίδραση μεταξύ των κοντινών αντικειμένων πράγματι διαμεσολαβείται.

Αποτελέσματα

Προτεινόμενη ρύθμιση

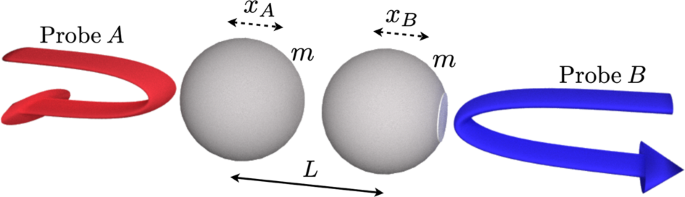
Εξετάστε δύο σωματίδια, χωρισμένα με απόσταση L , όπως απεικονίζεται στο σχήμα 1 . Στη συνέχεια, μελετάμε τη θέση όπου τα τεράστια σωματίδια κρατούνται ή απελευθερώνονται από τις μονοδιάστατες αρμονικές παγίδες. Στην πρώτη περίπτωση, μπορούμε να επεξεργαστούμε τα σωματίδια ως πανομοιότυπους αρμονικούς ταλαντωτές, με το ίδιο σχήμα, μάζα m , και συχνότητα ω vibration . Οι δύο ταλαντωτές και η βαρυτική αλληλεπίδραση μεταξύ τους δημιουργούν το σύνολο Χαμιλτονιανή H = H 0 + H g , όπου

{{} {{} {{} {{} {{} {{} {{}} { {A} ^ {2} + \ frac {{p} _ {B} ^ {2}} {2m} + \ frac {1} {2} {x} } ^ {2} $$

(1)

και H ζ περιγράφει τη βαρυτική όρο. Αν οι αρμονικές παγίδες αφαιρεθούν, ο αντίστοιχος Χ Hamiltonian απλοποιείται σε \ ({H} _ {0} = ({p} _ {A} ^ {2} + {p} _ {B} ^ {2} ) . Προτού προχωρήσουμε σε λεπτομερείς υπολογισμούς, θα συζητήσουμε τα γενικά χαρακτηριστικά του βαρυτικού όρου και τις προϋποθέσεις που απαιτούνται για τη δημιουργία εμπλοκής.