Sunday, September 13, 2020
Δρ. Μάνος Δανέζης «Βαρυτικά Κύματα μελετώντας την αόρατη θάλασσα του Κε...
Κβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Numerical simulation of a heavy black-hole merger with horizon deformati...
Κβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Για να φτιάξετε μια μηχανή μεγέθους ατόμου, χρειάζεστε έναν κβαντικό μηχανικό | EurekAlert! Επιστημονικά νέα
Για να φτιάξετε μια μηχανή μεγέθους ατόμου, χρειάζεστε έναν κβαντικό μηχανικό | EurekAlert! Επιστημονικά νέα: Here's a new chapter in the story of the miniaturisation of machines: researchers in a laboratory in Singapore have shown that a single atom can function as either an engine or a fridge. Such a device could be engineered into future computers and fuel cells to control energy flows.
Κβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
Κβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Saturday, September 12, 2020
Δυναμική χωροχρονικών φωτοκαρδιογράφων Ultrafast κοντά σε επιφάνειες GaN που μελετήθηκαν με φασματοσκοπία εκπομπών terahertz
Αφηρημένη
Το νιτρίδιο Gallium (GaN) είναι ένας πολλά υποσχόμενος ημιαγωγός ευρείας ζώνης και χρειάζονται νέα εργαλεία χαρακτηρισμού για τη μελέτη της τοπικής κρυσταλλικότητάς του, της δυναμικής του φορέα και των επιδράσεων ντόπινγκ. Η φασματοσκοπία εκπομπών Terahertz (THz) είναι μια αναδυόμενη πειραματική τεχνική που μπορεί να ανιχνεύσει την εξαιρετικά γρήγορη δυναμική του φορέα σε οπτικά διεγερμένους ημιαγωγούς. Σε αυτήν την εργασία, η δυναμική του φορέα και οι μηχανισμοί εκπομπών THz του GaN εξετάστηκαν σε ακούσια ντοπαρισμένα n-type, Si-doped n-type και Mg-doped p-type GaN. Οι φωτοφόροι φορείς διεγείρονται κοντά στην επιφάνεια ταξιδεύουν από την περιοχή διέγερσης με εξαιρετικά γρήγορο τρόπο και παράγουν ακτινοβολία THz σύμφωνα με το χρονικό παράγωγο του ρεύματος μετατόπισης κύματος. Η πολικότητα του πλάτους THz μπορεί να χρησιμοποιηθεί για τον προσδιορισμό του πλειοψηφικού τύπου φορέα σε ταινίες GaN μέσω μιας μεθόδου μη επαφής και μη καταστροφής.
Το νιτρίδιο Gallium (GaN) είναι ένας από τους πιο σημαντικούς ημιαγωγούς ευρείας ζώνης, που προσελκύει αξιοσημείωτο ενδιαφέρον για συσκευές εκπομπής φωτός, υψηλής ισχύος και υψηλής συχνότητας 1 , 2 . Παρά τις μεγάλες προσπάθειες, εξακολουθούν να υπάρχουν πολλά προβλήματα ποιότητας, όπως αναποτελεσματικό ντόπινγκ, ελαττώματα, καταστάσεις επιφάνειας και ελαττώματα παθητικοποίησης, τα οποία εμφανίζονται τόσο στους κρυστάλλους όσο και στις ταινίες 3 , 4 . Για παράδειγμα, υπάρχει φυσικά μια ισχυρή αυθόρμητη πόλωση στην όψη Ga του GaN κατά μήκος της κατεύθυνσης του άξονα c 5 . Λόγω αυτής της πόλωσης και των ελαττωμάτων στο GaN, ένα τυπικό τρανζίστορ υψηλής κινητικότητας AlGaN / GaN (HEMT) λειτουργεί ως συσκευή κανονικής λειτουργίας (λειτουργία εξάντλησης) ή πρέπει να λειτουργεί με οπίσθια πύλη 6 ,7 . Υπάρχουν ακόμη πολλές προκλήσεις που πρέπει να ξεπεραστούν για την επίτευξη καλύτερων συσκευών και υλικών GaN και νέα εργαλεία χαρακτηρισμού υλικού είναι ζωτικής σημασίας για την προώθηση της έρευνας σε αυτόν τον τομέα.
Η φασματοσκοπία εκπομπών Terahertz (THz) και ένα σύστημα απεικόνισης γνωστό ως μικροσκόπιο εκπομπών THz με λέιζερ (LTEM) είναι αναδυόμενα εργαλεία που χρησιμοποιούνται για τη μελέτη της εξαιρετικά γρήγορης κίνησης και μετατόπισης δυναμικών φορέων σε οπτικά διεγερμένα υλικά 8 , 9 . Πρόσφατα, καταδείξαμε την εφαρμογή του LTEM σε διάφορους ημιαγωγούς 10 , 11 , 12. Το LTEM χρησιμοποιεί λέιζερ femtosecond (fs) για να διεγείρει τους φορείς στα υλικά. Οι φορείς επιταχύνονται από ένα ηλεκτρικό πεδίο και διαχέονται από την περιοχή διέγερσης, η οποία προκαλεί ένα παροδικό ρεύμα, και τα κύματα THz εκπέμπονται σύμφωνα με το χρονικό παράγωγο του φωτορεύματος. Οι χρονικές κυματομορφές THz αντικατοπτρίζουν την εξαιρετικά γρήγορη δυναμική φορέα, οι οποίες βρίσκονται στο χρονοδιάγραμμα μερικών δεκάδων femtoseconds 13 .
Σε ημιαγωγούς ευρείας ζώνης, το βάθος διείσδυσης του φωτός είναι ρηχό, και οι περισσότεροι φωτοκατασκευαστές δημιουργούνται κοντά στην επιφάνεια του ημιαγωγού όταν η ενέργεια του φωτονίου είναι μεγαλύτερη από το εύρος ζώνης του ημιαγωγού. Η φωτοφωταύγεια (PL) και η ηλεκτροφωταύγεια μπορούν να χρησιμοποιηθούν για τον χαρακτηρισμό του ανασυνδυασμού φορέα που οδηγεί σε εκπομπές φωτονίων για χρόνους ανασυνδυασμού με τη σειρά των picoseconds έως nanoseconds. Οι Leitenstofer et al. έχει αποδείξει ότι, στο GaAs, το TES παρέχει πληροφορίες σχετικά με τη στιγμιαία φωτοαπόκριση αμέσως μετά την οπτική διέγερση 14 , 15, ενώ οι συμβατικές μέθοδοι παρέχουν πληροφορίες σχετικά με τη δυναμική του φορέα μετά την διάδοση του φορέα. Με το TES, μπορούν να ληφθούν πληροφορίες σχετικά με μηχανισμούς που εμφανίζονται σε χρονικές κλίμακες μικρότερες από ένα picosecond, όπως ταχύτητα και κατεύθυνση μετατόπισης φορέα.
Χρησιμοποιήθηκαν PL, απορρόφηση φωτονίων και μετρήσεις ανάκλασης αντλίας-ανιχνευτή για τη μελέτη της οπτικής απόκρισης του GaN, κυρίως παρέχοντας πληροφορίες σχετικά με ελαττώματα και σκέδαση φορέα. Στην παρούσα εργασία, το TES χρησιμοποιήθηκε για τη μελέτη των χωροχρονικών οπτικών αποκρίσεων του GaN. Γενικά, η εκπομπή THz από επιφάνειες ημιαγωγών προκαλείται από την επιτάχυνση των φωτοκαταφορέων από ένα ενσωματωμένο πεδίο κοντά στην επιφάνεια, όπως απεικονίζεται στο Σχήμα 1 , και / ή διάχυση φωτοκαταφορέα από την επιφάνεια στο μεγαλύτερο μέρος. Στην πρώτη περίπτωση, τα ηλεκτρόνια και οι οπές μετακινούνται προς την αντίθετη κατεύθυνση το ένα από το άλλο, και στην τελευταία περίπτωση, η διάχυση είναι προς την ίδια κατεύθυνση αλλά με διαφορετικές ταχύτητες, ένα φαινόμενο γνωστό ως φαινόμενο Photo-Dember 13 , 16 , 17 ,18 , 19 , το μοντέλο του οποίου χρησιμοποιείται συχνά για την εξήγηση του μηχανισμού εκπομπών THz από στενούς ημιαγωγούς. Δεδομένου ότι η κινητικότητα των ηλεκτρονίων στους ημιαγωγούς είναι μεγαλύτερη από αυτήν των οπών, συνεπώς, το TES αναμένεται να αποκαλύψει τέτοιες δυναμικές ηλεκτρονικές φωτοδιεγερμένες, και η πολικότητα των πλάτους κύματος THz θα υποδεικνύει τον πλειοψηφικό τύπο φορέα στους ημιαγωγούς GaN. Εδώ, εξετάσαμε ακούσια φιλμ ν-τύπου (# n-1), Si-doped n-type (# n-21) και Mg-doped p-type (# p-1) GaN για να λάβουμε μια σαφή κατανόηση Εκπομπή THz από την GaN. Οι κυματομορφές εκπομπών THz από τα δείγματα υπό διάφορες συνθήκες εξετάστηκαν και οι μηχανισμοί εκπομπών THz συζητούνται χρησιμοποιώντας το μοντέλο προσέγγισης βραχυπρόθεσμου από το Ref 20, μαζί με τις μετρήσεις PL και υπεριώδους ορατής απορρόφησης (UV-vis)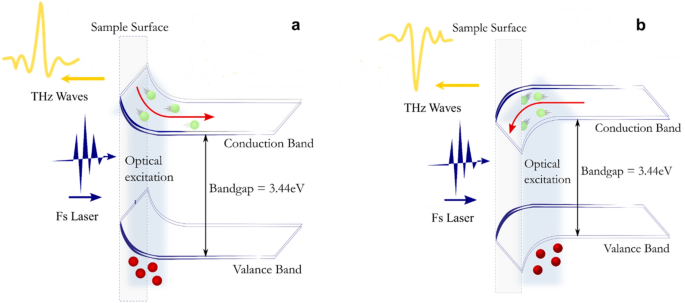

 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Saturday, August 29, 2020
Building a quantum computer at the SQMS Center at Fermilab
Κβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Monday, August 10, 2020
Building bespoke quantum hardware with superconducting circuits
ΚοσμολογίαΒασική ΦυσικήΓενική ΣχετικότηταΚβαντική Βαρύτητα ΒρόχουΠΟΛΥΜΕΣΑMultiverseΣωματιδίωνΗ ΦυσικηΚβαντική ΒαρύτηταΚβαντική ΦυσικήSpace-TimeΘεωρία ΧορδώνΘεωρητική Φυσική
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Sunday, August 09, 2020
Καταστάσεις πολλών φωτοτονίων από μια πηγή μονής φωτονίου στερεάς κατάστασης
Οι καταστάσεις φωτονικών γραφημάτων αποτελούν υποκείμενους πόρους για μονόδρομο οπτικό κβαντικό υπολογισμό, διόρθωση κβαντικών σφαλμάτων, θεμελιώδεις δοκιμές κβαντικής μηχανικής και κβαντικά δίκτυα επικοινωνίας. Τα περισσότερα υπάρχοντα έργα, ωστόσο, βασίζονται στις αυθόρμητες παραμετρικές πηγές μετατροπής που εγγενώς υποφέρουν από στοιχεία πιθανότητας δημιουργίας και διπλού ζεύγους. Εδώ, δημιουργούμε δύο σημαντικές κατηγορίες καταστάσεων γραφήματος, μια κατάσταση τεσσάρων φωτονίων με κωδικοποίηση πόλωσης Greenberger – Horne – Zeilinger (GHZ) και μια κατάσταση γραμμικής συστάδας, αποπολυπλέγοντας ενεργά μια ντετερμινιστική πηγή ενός φωτονίου από μια κβαντική κουκκίδα ημιαγωγού ενσωματωμένη σε ένα μικροπυλώνας. Μια κατάσταση πιστότητας 0,790 ± 0,009 (0,763 ± 0,004) και ρυθμός μέτρησης ∼13 Hz για την κατάσταση τεσσάρων φωτονίων GHZ (cluster)

 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Saturday, August 01, 2020
Συναντήσεις υψηλής ενέργειας με Black Hole
Μια προσέγγιση φυσικής σωματιδίων για την περιγραφή των αλληλεπιδράσεων των μαύρων οπών ανοίγει νέους δρόμους για την κατανόηση των παρατηρήσεων των βαρυτικών κυμάτων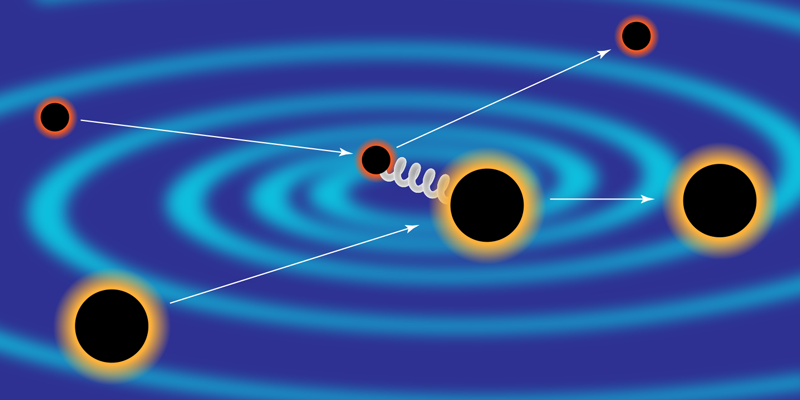 Σχήμα 1: Η σκέδαση της μαύρης τρύπας μπορεί να αντιμετωπιστεί ως αλληλεπίδραση τύπου σωματιδίων, στην οποία οι μαύρες τρύπες ανταλλάσσουν βαρύτητες. Υπολογίζοντας τα κβαντικά πλάτη σκέδασης, οι ερευνητές μπορούν να λάβουν σημαντικές πληροφορίες σχετικά με τη συγχώνευση δυαδικών μαύρων τρυπών που ... ΠερισσότεραΗ αστρονομία των βαρυτικών κυμάτων ακούγεται σαν επιστημονική φαντασία: δύο τεράστιες μαύρες τρύπες στροβιλίζονται η μία προς την άλλη σε ένα σημαντικό κλάσμα της ταχύτητας του φωτός, εκπέμποντας μια έκρηξη ενέργειας που υπερβαίνει τον Ήλιο με τη μορφή βαρυτικών κυμάτων. Εκατομμύρια έτη φωτός μακριά, στη Γη, παρατηρούμε αυτούς τους κυματισμούς στη γεωμετρία του χωροχρόνου μέσω των μικροσκοπικών παραμορφώσεων που παράγουν σε βραχίονες βραχιόνων χιλιομετρικών παρεμβολών [ 1]. Ένα κρίσιμο συστατικό για την ερμηνεία αυτών των σημάτων κύματος βαρύτητας είναι η ακριβής θεωρητική πρόβλεψη για τις παρατηρούμενες κυματομορφές, που λαμβάνονται μέσω της διαβόητα δύσκολης αποστολής επίλυσης των εξισώσεων πεδίου του Αϊνστάιν. Η μελλοντική πρόοδος εξαρτάται από τη σημαντική βελτίωση αυτών των θεωρητικών υπολογισμών, καθώς οι τρέχουσες προβλέψεις ενδέχεται να μην είναι αρκετά ακριβείς για τους αναβαθμισμένους ανιχνευτές που θα συνδεθούν στο διαδίκτυο το 2022 [ 2]. Εμπνευσμένη από τη φυσική των σωματιδίων, όπου τα πάντα είναι εννοιολογικά μειωμένα σε διεργασίες διασποράς μεταξύ σωματιδίων σημείου, ορισμένοι θεωρητικοί έχουν αρχίσει να επιτίθενται στο πρόβλημα των δυαδικών μαύρων τρυπών μελετώντας ένα σχετικό πρόβλημα στο οποίο δύο μαύρες τρύπες πετούν το ένα κοντά στο άλλο και παραμορφώνονται (διασκορπίζονται) από τους βαρυτική αλληλεπίδραση. Σε αυτό το πλαίσιο, ο Thibault Damour από το Ινστιτούτο Προηγμένων Επιστημονικών Σπουδών (IHÉS) στη Γαλλία και συνεργάτες του έχουν προκαλέσει απρόβλεπτη πρόοδο στις θεωρητικές προβλέψεις κύματος βαρύτητας [ 3 - 5 ]. Η τελευταία δουλειά τους δείχνει ότι υπάρχει μια υπολογιστική συντόμευση για το γενικό πρόβλημα σκέδασης, λαμβάνοντας υπόψη ένα ειδικό όριο όπου η μαύρη τρύπα ζυγίζει πολύ λιγότερο από την άλλη.
Η ανίχνευση βαρυτικών κυμάτων - καθώς και η εξαγωγή πληροφοριών πηγής (όπως μάζα, περιστροφή και τοποθεσία) και ο έλεγχος της θεμελιώδους φυσικής - βασίζεται σε μεγάλο βαθμό σε ακριβή θεωρητικά μοντέλα που χρησιμοποιούνται ως πρότυπα στην ανάλυση δεδομένων. Τόσο οι εξελιγμένες αριθμητικές προσομοιώσεις όσο και οι ανασταλτικοί αναλυτικοί υπολογισμοί είναι απαραίτητοι για αυτό το σκοπό και και οι δύο πρέπει να βελτιωθούν με ακρίβεια προκειμένου να αναλυθούν τα δεδομένα που θα προέλθουν από πρόσφατα βελτιωμένα παρατηρητήρια (LIGO, Virgo και KAGRA) και μελλοντικά όργανα (LISA, Cosmic Explorer , και το Τηλεσκόπιο του Αϊνστάιν) [ 2 ].
Στη θεωρία διαταραχών, οι εξισώσεις κίνησης γράφονται ως μια σειρά όρων που περιέχουν κάποια μικρή ποσότητα 𝜖 μεταφερθεί στις αυξανόμενες εξουσίες: πρώτη τάξη 𝜖, δεύτερη παραγγελία 𝜖2, τρίτη παραγγελία 𝜖3, κ.λπ. Το τοπίο των διαταραχών αναλυτικών μεθόδων μπορεί να χαρτογραφηθεί σύμφωνα με την ποσότητα που είναι μικρή: ένα αδύναμο βαρυτικό πεδίο (μετά την επέκταση του Minkowskian), ένα αδύναμο πεδίο και μαύρες τρύπες με αργή κίνηση (μετά την επέκταση του Νεύτωνα) ή μια μικρή αναλογία μάζας μεταξύ των μαύρων οπών (όπως στο πρόγραμμα βαρυτικής αυτο-δύναμης). Στο παρελθόν, η προσέγγιση μετά τον Μινκόφσκιν έλαβε τη λιγότερη προσοχή, καθώς είναι πιο χρήσιμη για τη διασπορά των μαύρων οπών - ένα γεγονός που κανονικά θα παρήγαγε πολύ μικρή βαρυτική ακτινοβολία για να παρατηρηθεί. Ωστόσο, οι θεωρητικοί συνειδητοποίησαν πρόσφατα ότι οι υπολογισμοί που έγιναν για τη διασπορά (μη δεσμευμένων) μαύρων οπών μπορούν να αποκαλύψουν σημαντικά στοιχεία, όπως το δυναμικό βαρύτητας, για συγχώνευση (δεσμευμένων) συστημάτων. Αυτή η σύνδεση έχει φέρει κοντά ερευνητές από τις κοινότητες κλασικής και κβαντικής βαρύτητας,
Η βασική ιδέα σε αυτήν την προσέγγιση σκέδασης είναι να αντιμετωπίζονται οι μαύρες τρύπες ως κβαντικά σωματίδια που αλληλεπιδρούν μέσω της ανταλλαγής βαρυτονίων, με τον ίδιο τρόπο που τα ηλεκτρόνια αλληλεπιδρούν μέσω της ανταλλαγής φωτονίων (Εικ. 1 ). Συνδυάζοντας όλους τους διαφορετικούς τρόπους με τους οποίους αλληλεπιδρούν τα σωματίδια, οι ερευνητές μπορούν να επιτύχουν εξαιρετικά ακριβείς προβλέψεις - όπως αποδεικνύεται από την πειραματική επιβεβαίωση έως και 12 ψηφίων της προβλεπόμενης ανώμαλης μαγνητικής διπόλης ροπής του ηλεκτρονίου [ 6]. Μια κρίσιμη κβαντική ιδέα είναι ότι τα πλάτη σκέδασης, που δίνουν την πιθανότητα για συγκεκριμένες διεργασίες σκέδασης, περιορίζονται έντονα από τις γενικές αρχές (συμμετρίες, τοποθεσία, διατήρηση της πιθανότητας). Αρκετές ομάδες εφαρμόζουν επί του παρόντος αυτές και άλλες ισχυρές τεχνικές από την κβαντική θεωρία πεδίου για να προσδιορίσουν τα πλάτη βαρυτικής σκέδασης μεταξύ «σωματιδίων μαύρης τρύπας». Τα πλάτη είναι κβαντικά παρατηρήσιμα, αλλά οι ερευνητές μπορούν να εξαγάγουν ένα κλασικό μέρος, το οποίο μπορεί να χρησιμοποιηθεί για την κατασκευή προτύπων για την ανάλυση βαρυτικών κυμάτων [ 7 ].
Η Damour ανακάλυψε μια απλή αλλά εκτεταμένη σύνδεση μεταξύ διαφορετικών προσεγγιστικών προσεγγίσεων σε κλασικούς υπολογισμούς σκέδασης μαύρων τρυπών [ 3 ]. Έχει δείξει ότι η μαζική εξάρτηση της κλασικής συνάρτησης γωνίας σκέδασης είναι τέτοια ώστε η συνάρτηση να μπορεί να σταθεροποιηθεί πλήρως σε μια συγκεκριμένη σειρά κατά την μετά-Μινκοβσσιανή προσέγγιση από χαμηλότερες τάξεις στην προσέγγιση αυτο-δύναμης (μικρός-λόγος μάζας). Αυτό το εύρημα είναι ισχυρό αφού η τελευταία προσέγγιση χρησιμοποιεί πλήρως τις ακριβείς (μη γραμμικές) λύσεις μαύρης τρύπας στην κλασική βαρύτητα του Αϊνστάιν. Για παράδειγμα, σύμφωνα με τα ευρήματα του Νταμούρ, η τέταρτη σειρά στην προσέγγιση μετά τον Μινκοβσκόνια - μία σειρά πάνω από τον υπερσύγχρονο υπολογισμό κβαντικού πλάτους που επιτεύχθηκε από τη Zvi Bern και συνεργάτες [ 7] - θα μπορούσε να προσδιοριστεί μόνο από τους υπολογισμούς αυτοβίας πρώτης τάξης. Αυτή η συντόμευση θα μπορούσε να επιταχύνει τις προσπάθειες για την επίτευξη προβλέψεων υψηλότερης τάξης (πιο ακριβείς) στο μέλλον. Ήδη, ο Damour και οι συνάδελφοί του έχουν χρησιμοποιήσει υπολογισμούς αυτοβίας πρώτης τάξεως για να προσδιορίσουν μεγάλα τμήματα της συντηρητικής δυναμικής πέμπτης έως έκτης τάξης, που απαιτούνται για τον προσδιορισμό του δυναμικού βαρύτητας στα δεσμευμένα συστήματα [ 4 , 5 , 8 ]. Μερικοί από τους όρους σε αυτούς τους υπολογισμούς έχουν συζητηθεί έντονα και αποτέλεσαν αντικείμενο φιλικού στοιχήματος μεταξύ της Βέρνης και της Νταμούρ [ 9 ], την οποία δέχτηκε πρόσφατα ο Νταμούρ [ 5 ].
Ενώ η προώθηση των διαταραχών υψηλής τάξης είναι σίγουρα σημαντική, η Damour έχει επίσης προκαλέσει την κοινότητα θέτοντας ζητήματα σχετικά με τις θεμελιώδεις πτυχές της κβαντικής βαρυτικής έρευνας σκέδασης [ 3 ]. Έχει θέσει πολλές λεπτές ερωτήσεις: Έχει νόημα να αναγνωρίσουμε ένα κλασικό μέρος ενός πλάτους σκέδασης, το οποίο είναι συνήθως ένα πιθανό κβαντικό παρατηρούμενο χωρίς άμεσο κλασικό ανάλογο; Πόσο ακριβώς προσθέτει η ανταλλαγή βαρυτών σε μεγάλες κλασικές γωνίες εκτροπής; Πώς σχετίζεται η κλασική σκέδαση της μαύρης τρύπας στο όριο υψηλής ενέργειας με τα κβαντικά αποτελέσματα για τη διασπορά σωματιδίων χωρίς μάζα [ 10 , 11 ]; Η επίλυση αυτών των ζητημάτων θα μπορούσε να βοηθήσει τους ερευνητές να χαρτογραφήσουν μελλοντικούς δρόμους για να κάνουν πιο ακριβείς προβλέψεις.
Η μελέτη της διασποράς των μαύρων τρυπών έχει γίνει μια πολλά υποσχόμενη ερευνητική κατεύθυνση, προσελκύοντας διαφορετικές ομάδες που εργάζονται σε ένα ευρύ φάσμα μεθοδολογιών. Οι πιο πρόσφατες προσπάθειες [ 3 - 5 , 7 , 8 , 12 ] καταδεικνύουν τις δυνατότητες αυτής της προσέγγισης για την επιστήμη των βαρυτικών κυμάτων: Οι ακριβέστερες προβλέψεις σε υψηλές τάξεις στη θεωρία διαταραχών έρχονται προσιτές και η περαιτέρω πρόοδος σε αυτόν τον τομέα μπορεί να βελτιώσει σημαντικά επιστημονική ικανότητα των μελλοντικών παρατηρητηρίων βαρυτικών κυμάτων. Επιπλέον, η αντιπαράθεση διαφορετικών κοινοτήτων και οι τρόποι σκέψης τους φέρουν απρόβλεπτες ευκαιρίες για θεωρητικές ανακαλύψεις, ακόμη και πέρα από τα βαρυτικά κύματα. Ήρθε η ώρα να περάσει αυτός ο ορίζοντας.
Η έρευνα δημοσιεύεται στο περιοδικό Physical Review D .
Σχήμα 1: Η σκέδαση της μαύρης τρύπας μπορεί να αντιμετωπιστεί ως αλληλεπίδραση τύπου σωματιδίων, στην οποία οι μαύρες τρύπες ανταλλάσσουν βαρύτητες. Υπολογίζοντας τα κβαντικά πλάτη σκέδασης, οι ερευνητές μπορούν να λάβουν σημαντικές πληροφορίες σχετικά με τη συγχώνευση δυαδικών μαύρων τρυπών που ... ΠερισσότεραΗ αστρονομία των βαρυτικών κυμάτων ακούγεται σαν επιστημονική φαντασία: δύο τεράστιες μαύρες τρύπες στροβιλίζονται η μία προς την άλλη σε ένα σημαντικό κλάσμα της ταχύτητας του φωτός, εκπέμποντας μια έκρηξη ενέργειας που υπερβαίνει τον Ήλιο με τη μορφή βαρυτικών κυμάτων. Εκατομμύρια έτη φωτός μακριά, στη Γη, παρατηρούμε αυτούς τους κυματισμούς στη γεωμετρία του χωροχρόνου μέσω των μικροσκοπικών παραμορφώσεων που παράγουν σε βραχίονες βραχιόνων χιλιομετρικών παρεμβολών [ 1]. Ένα κρίσιμο συστατικό για την ερμηνεία αυτών των σημάτων κύματος βαρύτητας είναι η ακριβής θεωρητική πρόβλεψη για τις παρατηρούμενες κυματομορφές, που λαμβάνονται μέσω της διαβόητα δύσκολης αποστολής επίλυσης των εξισώσεων πεδίου του Αϊνστάιν. Η μελλοντική πρόοδος εξαρτάται από τη σημαντική βελτίωση αυτών των θεωρητικών υπολογισμών, καθώς οι τρέχουσες προβλέψεις ενδέχεται να μην είναι αρκετά ακριβείς για τους αναβαθμισμένους ανιχνευτές που θα συνδεθούν στο διαδίκτυο το 2022 [ 2]. Εμπνευσμένη από τη φυσική των σωματιδίων, όπου τα πάντα είναι εννοιολογικά μειωμένα σε διεργασίες διασποράς μεταξύ σωματιδίων σημείου, ορισμένοι θεωρητικοί έχουν αρχίσει να επιτίθενται στο πρόβλημα των δυαδικών μαύρων τρυπών μελετώντας ένα σχετικό πρόβλημα στο οποίο δύο μαύρες τρύπες πετούν το ένα κοντά στο άλλο και παραμορφώνονται (διασκορπίζονται) από τους βαρυτική αλληλεπίδραση. Σε αυτό το πλαίσιο, ο Thibault Damour από το Ινστιτούτο Προηγμένων Επιστημονικών Σπουδών (IHÉS) στη Γαλλία και συνεργάτες του έχουν προκαλέσει απρόβλεπτη πρόοδο στις θεωρητικές προβλέψεις κύματος βαρύτητας [ 3 - 5 ]. Η τελευταία δουλειά τους δείχνει ότι υπάρχει μια υπολογιστική συντόμευση για το γενικό πρόβλημα σκέδασης, λαμβάνοντας υπόψη ένα ειδικό όριο όπου η μαύρη τρύπα ζυγίζει πολύ λιγότερο από την άλλη.
Η ανίχνευση βαρυτικών κυμάτων - καθώς και η εξαγωγή πληροφοριών πηγής (όπως μάζα, περιστροφή και τοποθεσία) και ο έλεγχος της θεμελιώδους φυσικής - βασίζεται σε μεγάλο βαθμό σε ακριβή θεωρητικά μοντέλα που χρησιμοποιούνται ως πρότυπα στην ανάλυση δεδομένων. Τόσο οι εξελιγμένες αριθμητικές προσομοιώσεις όσο και οι ανασταλτικοί αναλυτικοί υπολογισμοί είναι απαραίτητοι για αυτό το σκοπό και και οι δύο πρέπει να βελτιωθούν με ακρίβεια προκειμένου να αναλυθούν τα δεδομένα που θα προέλθουν από πρόσφατα βελτιωμένα παρατηρητήρια (LIGO, Virgo και KAGRA) και μελλοντικά όργανα (LISA, Cosmic Explorer , και το Τηλεσκόπιο του Αϊνστάιν) [ 2 ].
Στη θεωρία διαταραχών, οι εξισώσεις κίνησης γράφονται ως μια σειρά όρων που περιέχουν κάποια μικρή ποσότητα 𝜖 μεταφερθεί στις αυξανόμενες εξουσίες: πρώτη τάξη 𝜖, δεύτερη παραγγελία 𝜖2, τρίτη παραγγελία 𝜖3, κ.λπ. Το τοπίο των διαταραχών αναλυτικών μεθόδων μπορεί να χαρτογραφηθεί σύμφωνα με την ποσότητα που είναι μικρή: ένα αδύναμο βαρυτικό πεδίο (μετά την επέκταση του Minkowskian), ένα αδύναμο πεδίο και μαύρες τρύπες με αργή κίνηση (μετά την επέκταση του Νεύτωνα) ή μια μικρή αναλογία μάζας μεταξύ των μαύρων οπών (όπως στο πρόγραμμα βαρυτικής αυτο-δύναμης). Στο παρελθόν, η προσέγγιση μετά τον Μινκόφσκιν έλαβε τη λιγότερη προσοχή, καθώς είναι πιο χρήσιμη για τη διασπορά των μαύρων οπών - ένα γεγονός που κανονικά θα παρήγαγε πολύ μικρή βαρυτική ακτινοβολία για να παρατηρηθεί. Ωστόσο, οι θεωρητικοί συνειδητοποίησαν πρόσφατα ότι οι υπολογισμοί που έγιναν για τη διασπορά (μη δεσμευμένων) μαύρων οπών μπορούν να αποκαλύψουν σημαντικά στοιχεία, όπως το δυναμικό βαρύτητας, για συγχώνευση (δεσμευμένων) συστημάτων. Αυτή η σύνδεση έχει φέρει κοντά ερευνητές από τις κοινότητες κλασικής και κβαντικής βαρύτητας,
Η βασική ιδέα σε αυτήν την προσέγγιση σκέδασης είναι να αντιμετωπίζονται οι μαύρες τρύπες ως κβαντικά σωματίδια που αλληλεπιδρούν μέσω της ανταλλαγής βαρυτονίων, με τον ίδιο τρόπο που τα ηλεκτρόνια αλληλεπιδρούν μέσω της ανταλλαγής φωτονίων (Εικ. 1 ). Συνδυάζοντας όλους τους διαφορετικούς τρόπους με τους οποίους αλληλεπιδρούν τα σωματίδια, οι ερευνητές μπορούν να επιτύχουν εξαιρετικά ακριβείς προβλέψεις - όπως αποδεικνύεται από την πειραματική επιβεβαίωση έως και 12 ψηφίων της προβλεπόμενης ανώμαλης μαγνητικής διπόλης ροπής του ηλεκτρονίου [ 6]. Μια κρίσιμη κβαντική ιδέα είναι ότι τα πλάτη σκέδασης, που δίνουν την πιθανότητα για συγκεκριμένες διεργασίες σκέδασης, περιορίζονται έντονα από τις γενικές αρχές (συμμετρίες, τοποθεσία, διατήρηση της πιθανότητας). Αρκετές ομάδες εφαρμόζουν επί του παρόντος αυτές και άλλες ισχυρές τεχνικές από την κβαντική θεωρία πεδίου για να προσδιορίσουν τα πλάτη βαρυτικής σκέδασης μεταξύ «σωματιδίων μαύρης τρύπας». Τα πλάτη είναι κβαντικά παρατηρήσιμα, αλλά οι ερευνητές μπορούν να εξαγάγουν ένα κλασικό μέρος, το οποίο μπορεί να χρησιμοποιηθεί για την κατασκευή προτύπων για την ανάλυση βαρυτικών κυμάτων [ 7 ].
Η Damour ανακάλυψε μια απλή αλλά εκτεταμένη σύνδεση μεταξύ διαφορετικών προσεγγιστικών προσεγγίσεων σε κλασικούς υπολογισμούς σκέδασης μαύρων τρυπών [ 3 ]. Έχει δείξει ότι η μαζική εξάρτηση της κλασικής συνάρτησης γωνίας σκέδασης είναι τέτοια ώστε η συνάρτηση να μπορεί να σταθεροποιηθεί πλήρως σε μια συγκεκριμένη σειρά κατά την μετά-Μινκοβσσιανή προσέγγιση από χαμηλότερες τάξεις στην προσέγγιση αυτο-δύναμης (μικρός-λόγος μάζας). Αυτό το εύρημα είναι ισχυρό αφού η τελευταία προσέγγιση χρησιμοποιεί πλήρως τις ακριβείς (μη γραμμικές) λύσεις μαύρης τρύπας στην κλασική βαρύτητα του Αϊνστάιν. Για παράδειγμα, σύμφωνα με τα ευρήματα του Νταμούρ, η τέταρτη σειρά στην προσέγγιση μετά τον Μινκοβσκόνια - μία σειρά πάνω από τον υπερσύγχρονο υπολογισμό κβαντικού πλάτους που επιτεύχθηκε από τη Zvi Bern και συνεργάτες [ 7] - θα μπορούσε να προσδιοριστεί μόνο από τους υπολογισμούς αυτοβίας πρώτης τάξης. Αυτή η συντόμευση θα μπορούσε να επιταχύνει τις προσπάθειες για την επίτευξη προβλέψεων υψηλότερης τάξης (πιο ακριβείς) στο μέλλον. Ήδη, ο Damour και οι συνάδελφοί του έχουν χρησιμοποιήσει υπολογισμούς αυτοβίας πρώτης τάξεως για να προσδιορίσουν μεγάλα τμήματα της συντηρητικής δυναμικής πέμπτης έως έκτης τάξης, που απαιτούνται για τον προσδιορισμό του δυναμικού βαρύτητας στα δεσμευμένα συστήματα [ 4 , 5 , 8 ]. Μερικοί από τους όρους σε αυτούς τους υπολογισμούς έχουν συζητηθεί έντονα και αποτέλεσαν αντικείμενο φιλικού στοιχήματος μεταξύ της Βέρνης και της Νταμούρ [ 9 ], την οποία δέχτηκε πρόσφατα ο Νταμούρ [ 5 ].
Ενώ η προώθηση των διαταραχών υψηλής τάξης είναι σίγουρα σημαντική, η Damour έχει επίσης προκαλέσει την κοινότητα θέτοντας ζητήματα σχετικά με τις θεμελιώδεις πτυχές της κβαντικής βαρυτικής έρευνας σκέδασης [ 3 ]. Έχει θέσει πολλές λεπτές ερωτήσεις: Έχει νόημα να αναγνωρίσουμε ένα κλασικό μέρος ενός πλάτους σκέδασης, το οποίο είναι συνήθως ένα πιθανό κβαντικό παρατηρούμενο χωρίς άμεσο κλασικό ανάλογο; Πόσο ακριβώς προσθέτει η ανταλλαγή βαρυτών σε μεγάλες κλασικές γωνίες εκτροπής; Πώς σχετίζεται η κλασική σκέδαση της μαύρης τρύπας στο όριο υψηλής ενέργειας με τα κβαντικά αποτελέσματα για τη διασπορά σωματιδίων χωρίς μάζα [ 10 , 11 ]; Η επίλυση αυτών των ζητημάτων θα μπορούσε να βοηθήσει τους ερευνητές να χαρτογραφήσουν μελλοντικούς δρόμους για να κάνουν πιο ακριβείς προβλέψεις.
Η μελέτη της διασποράς των μαύρων τρυπών έχει γίνει μια πολλά υποσχόμενη ερευνητική κατεύθυνση, προσελκύοντας διαφορετικές ομάδες που εργάζονται σε ένα ευρύ φάσμα μεθοδολογιών. Οι πιο πρόσφατες προσπάθειες [ 3 - 5 , 7 , 8 , 12 ] καταδεικνύουν τις δυνατότητες αυτής της προσέγγισης για την επιστήμη των βαρυτικών κυμάτων: Οι ακριβέστερες προβλέψεις σε υψηλές τάξεις στη θεωρία διαταραχών έρχονται προσιτές και η περαιτέρω πρόοδος σε αυτόν τον τομέα μπορεί να βελτιώσει σημαντικά επιστημονική ικανότητα των μελλοντικών παρατηρητηρίων βαρυτικών κυμάτων. Επιπλέον, η αντιπαράθεση διαφορετικών κοινοτήτων και οι τρόποι σκέψης τους φέρουν απρόβλεπτες ευκαιρίες για θεωρητικές ανακαλύψεις, ακόμη και πέρα από τα βαρυτικά κύματα. Ήρθε η ώρα να περάσει αυτός ο ορίζοντας.
Η έρευνα δημοσιεύεται στο περιοδικό Physical Review D .
 Σχήμα 1: Η σκέδαση της μαύρης τρύπας μπορεί να αντιμετωπιστεί ως αλληλεπίδραση τύπου σωματιδίων, στην οποία οι μαύρες τρύπες ανταλλάσσουν βαρύτητες. Υπολογίζοντας τα κβαντικά πλάτη σκέδασης, οι ερευνητές μπορούν να λάβουν σημαντικές πληροφορίες σχετικά με τη συγχώνευση δυαδικών μαύρων τρυπών που ... ΠερισσότεραΗ αστρονομία των βαρυτικών κυμάτων ακούγεται σαν επιστημονική φαντασία: δύο τεράστιες μαύρες τρύπες στροβιλίζονται η μία προς την άλλη σε ένα σημαντικό κλάσμα της ταχύτητας του φωτός, εκπέμποντας μια έκρηξη ενέργειας που υπερβαίνει τον Ήλιο με τη μορφή βαρυτικών κυμάτων. Εκατομμύρια έτη φωτός μακριά, στη Γη, παρατηρούμε αυτούς τους κυματισμούς στη γεωμετρία του χωροχρόνου μέσω των μικροσκοπικών παραμορφώσεων που παράγουν σε βραχίονες βραχιόνων χιλιομετρικών παρεμβολών [ 1]. Ένα κρίσιμο συστατικό για την ερμηνεία αυτών των σημάτων κύματος βαρύτητας είναι η ακριβής θεωρητική πρόβλεψη για τις παρατηρούμενες κυματομορφές, που λαμβάνονται μέσω της διαβόητα δύσκολης αποστολής επίλυσης των εξισώσεων πεδίου του Αϊνστάιν. Η μελλοντική πρόοδος εξαρτάται από τη σημαντική βελτίωση αυτών των θεωρητικών υπολογισμών, καθώς οι τρέχουσες προβλέψεις ενδέχεται να μην είναι αρκετά ακριβείς για τους αναβαθμισμένους ανιχνευτές που θα συνδεθούν στο διαδίκτυο το 2022 [ 2]. Εμπνευσμένη από τη φυσική των σωματιδίων, όπου τα πάντα είναι εννοιολογικά μειωμένα σε διεργασίες διασποράς μεταξύ σωματιδίων σημείου, ορισμένοι θεωρητικοί έχουν αρχίσει να επιτίθενται στο πρόβλημα των δυαδικών μαύρων τρυπών μελετώντας ένα σχετικό πρόβλημα στο οποίο δύο μαύρες τρύπες πετούν το ένα κοντά στο άλλο και παραμορφώνονται (διασκορπίζονται) από τους βαρυτική αλληλεπίδραση. Σε αυτό το πλαίσιο, ο Thibault Damour από το Ινστιτούτο Προηγμένων Επιστημονικών Σπουδών (IHÉS) στη Γαλλία και συνεργάτες του έχουν προκαλέσει απρόβλεπτη πρόοδο στις θεωρητικές προβλέψεις κύματος βαρύτητας [ 3 - 5 ]. Η τελευταία δουλειά τους δείχνει ότι υπάρχει μια υπολογιστική συντόμευση για το γενικό πρόβλημα σκέδασης, λαμβάνοντας υπόψη ένα ειδικό όριο όπου η μαύρη τρύπα ζυγίζει πολύ λιγότερο από την άλλη.
Η ανίχνευση βαρυτικών κυμάτων - καθώς και η εξαγωγή πληροφοριών πηγής (όπως μάζα, περιστροφή και τοποθεσία) και ο έλεγχος της θεμελιώδους φυσικής - βασίζεται σε μεγάλο βαθμό σε ακριβή θεωρητικά μοντέλα που χρησιμοποιούνται ως πρότυπα στην ανάλυση δεδομένων. Τόσο οι εξελιγμένες αριθμητικές προσομοιώσεις όσο και οι ανασταλτικοί αναλυτικοί υπολογισμοί είναι απαραίτητοι για αυτό το σκοπό και και οι δύο πρέπει να βελτιωθούν με ακρίβεια προκειμένου να αναλυθούν τα δεδομένα που θα προέλθουν από πρόσφατα βελτιωμένα παρατηρητήρια (LIGO, Virgo και KAGRA) και μελλοντικά όργανα (LISA, Cosmic Explorer , και το Τηλεσκόπιο του Αϊνστάιν) [ 2 ].
Στη θεωρία διαταραχών, οι εξισώσεις κίνησης γράφονται ως μια σειρά όρων που περιέχουν κάποια μικρή ποσότητα 𝜖 μεταφερθεί στις αυξανόμενες εξουσίες: πρώτη τάξη 𝜖, δεύτερη παραγγελία 𝜖2, τρίτη παραγγελία 𝜖3, κ.λπ. Το τοπίο των διαταραχών αναλυτικών μεθόδων μπορεί να χαρτογραφηθεί σύμφωνα με την ποσότητα που είναι μικρή: ένα αδύναμο βαρυτικό πεδίο (μετά την επέκταση του Minkowskian), ένα αδύναμο πεδίο και μαύρες τρύπες με αργή κίνηση (μετά την επέκταση του Νεύτωνα) ή μια μικρή αναλογία μάζας μεταξύ των μαύρων οπών (όπως στο πρόγραμμα βαρυτικής αυτο-δύναμης). Στο παρελθόν, η προσέγγιση μετά τον Μινκόφσκιν έλαβε τη λιγότερη προσοχή, καθώς είναι πιο χρήσιμη για τη διασπορά των μαύρων οπών - ένα γεγονός που κανονικά θα παρήγαγε πολύ μικρή βαρυτική ακτινοβολία για να παρατηρηθεί. Ωστόσο, οι θεωρητικοί συνειδητοποίησαν πρόσφατα ότι οι υπολογισμοί που έγιναν για τη διασπορά (μη δεσμευμένων) μαύρων οπών μπορούν να αποκαλύψουν σημαντικά στοιχεία, όπως το δυναμικό βαρύτητας, για συγχώνευση (δεσμευμένων) συστημάτων. Αυτή η σύνδεση έχει φέρει κοντά ερευνητές από τις κοινότητες κλασικής και κβαντικής βαρύτητας,
Η βασική ιδέα σε αυτήν την προσέγγιση σκέδασης είναι να αντιμετωπίζονται οι μαύρες τρύπες ως κβαντικά σωματίδια που αλληλεπιδρούν μέσω της ανταλλαγής βαρυτονίων, με τον ίδιο τρόπο που τα ηλεκτρόνια αλληλεπιδρούν μέσω της ανταλλαγής φωτονίων (Εικ. 1 ). Συνδυάζοντας όλους τους διαφορετικούς τρόπους με τους οποίους αλληλεπιδρούν τα σωματίδια, οι ερευνητές μπορούν να επιτύχουν εξαιρετικά ακριβείς προβλέψεις - όπως αποδεικνύεται από την πειραματική επιβεβαίωση έως και 12 ψηφίων της προβλεπόμενης ανώμαλης μαγνητικής διπόλης ροπής του ηλεκτρονίου [ 6]. Μια κρίσιμη κβαντική ιδέα είναι ότι τα πλάτη σκέδασης, που δίνουν την πιθανότητα για συγκεκριμένες διεργασίες σκέδασης, περιορίζονται έντονα από τις γενικές αρχές (συμμετρίες, τοποθεσία, διατήρηση της πιθανότητας). Αρκετές ομάδες εφαρμόζουν επί του παρόντος αυτές και άλλες ισχυρές τεχνικές από την κβαντική θεωρία πεδίου για να προσδιορίσουν τα πλάτη βαρυτικής σκέδασης μεταξύ «σωματιδίων μαύρης τρύπας». Τα πλάτη είναι κβαντικά παρατηρήσιμα, αλλά οι ερευνητές μπορούν να εξαγάγουν ένα κλασικό μέρος, το οποίο μπορεί να χρησιμοποιηθεί για την κατασκευή προτύπων για την ανάλυση βαρυτικών κυμάτων [ 7 ].
Η Damour ανακάλυψε μια απλή αλλά εκτεταμένη σύνδεση μεταξύ διαφορετικών προσεγγιστικών προσεγγίσεων σε κλασικούς υπολογισμούς σκέδασης μαύρων τρυπών [ 3 ]. Έχει δείξει ότι η μαζική εξάρτηση της κλασικής συνάρτησης γωνίας σκέδασης είναι τέτοια ώστε η συνάρτηση να μπορεί να σταθεροποιηθεί πλήρως σε μια συγκεκριμένη σειρά κατά την μετά-Μινκοβσσιανή προσέγγιση από χαμηλότερες τάξεις στην προσέγγιση αυτο-δύναμης (μικρός-λόγος μάζας). Αυτό το εύρημα είναι ισχυρό αφού η τελευταία προσέγγιση χρησιμοποιεί πλήρως τις ακριβείς (μη γραμμικές) λύσεις μαύρης τρύπας στην κλασική βαρύτητα του Αϊνστάιν. Για παράδειγμα, σύμφωνα με τα ευρήματα του Νταμούρ, η τέταρτη σειρά στην προσέγγιση μετά τον Μινκοβσκόνια - μία σειρά πάνω από τον υπερσύγχρονο υπολογισμό κβαντικού πλάτους που επιτεύχθηκε από τη Zvi Bern και συνεργάτες [ 7] - θα μπορούσε να προσδιοριστεί μόνο από τους υπολογισμούς αυτοβίας πρώτης τάξης. Αυτή η συντόμευση θα μπορούσε να επιταχύνει τις προσπάθειες για την επίτευξη προβλέψεων υψηλότερης τάξης (πιο ακριβείς) στο μέλλον. Ήδη, ο Damour και οι συνάδελφοί του έχουν χρησιμοποιήσει υπολογισμούς αυτοβίας πρώτης τάξεως για να προσδιορίσουν μεγάλα τμήματα της συντηρητικής δυναμικής πέμπτης έως έκτης τάξης, που απαιτούνται για τον προσδιορισμό του δυναμικού βαρύτητας στα δεσμευμένα συστήματα [ 4 , 5 , 8 ]. Μερικοί από τους όρους σε αυτούς τους υπολογισμούς έχουν συζητηθεί έντονα και αποτέλεσαν αντικείμενο φιλικού στοιχήματος μεταξύ της Βέρνης και της Νταμούρ [ 9 ], την οποία δέχτηκε πρόσφατα ο Νταμούρ [ 5 ].
Ενώ η προώθηση των διαταραχών υψηλής τάξης είναι σίγουρα σημαντική, η Damour έχει επίσης προκαλέσει την κοινότητα θέτοντας ζητήματα σχετικά με τις θεμελιώδεις πτυχές της κβαντικής βαρυτικής έρευνας σκέδασης [ 3 ]. Έχει θέσει πολλές λεπτές ερωτήσεις: Έχει νόημα να αναγνωρίσουμε ένα κλασικό μέρος ενός πλάτους σκέδασης, το οποίο είναι συνήθως ένα πιθανό κβαντικό παρατηρούμενο χωρίς άμεσο κλασικό ανάλογο; Πόσο ακριβώς προσθέτει η ανταλλαγή βαρυτών σε μεγάλες κλασικές γωνίες εκτροπής; Πώς σχετίζεται η κλασική σκέδαση της μαύρης τρύπας στο όριο υψηλής ενέργειας με τα κβαντικά αποτελέσματα για τη διασπορά σωματιδίων χωρίς μάζα [ 10 , 11 ]; Η επίλυση αυτών των ζητημάτων θα μπορούσε να βοηθήσει τους ερευνητές να χαρτογραφήσουν μελλοντικούς δρόμους για να κάνουν πιο ακριβείς προβλέψεις.
Η μελέτη της διασποράς των μαύρων τρυπών έχει γίνει μια πολλά υποσχόμενη ερευνητική κατεύθυνση, προσελκύοντας διαφορετικές ομάδες που εργάζονται σε ένα ευρύ φάσμα μεθοδολογιών. Οι πιο πρόσφατες προσπάθειες [ 3 - 5 , 7 , 8 , 12 ] καταδεικνύουν τις δυνατότητες αυτής της προσέγγισης για την επιστήμη των βαρυτικών κυμάτων: Οι ακριβέστερες προβλέψεις σε υψηλές τάξεις στη θεωρία διαταραχών έρχονται προσιτές και η περαιτέρω πρόοδος σε αυτόν τον τομέα μπορεί να βελτιώσει σημαντικά επιστημονική ικανότητα των μελλοντικών παρατηρητηρίων βαρυτικών κυμάτων. Επιπλέον, η αντιπαράθεση διαφορετικών κοινοτήτων και οι τρόποι σκέψης τους φέρουν απρόβλεπτες ευκαιρίες για θεωρητικές ανακαλύψεις, ακόμη και πέρα από τα βαρυτικά κύματα. Ήρθε η ώρα να περάσει αυτός ο ορίζοντας.
Η έρευνα δημοσιεύεται στο περιοδικό Physical Review D .
Σχήμα 1: Η σκέδαση της μαύρης τρύπας μπορεί να αντιμετωπιστεί ως αλληλεπίδραση τύπου σωματιδίων, στην οποία οι μαύρες τρύπες ανταλλάσσουν βαρύτητες. Υπολογίζοντας τα κβαντικά πλάτη σκέδασης, οι ερευνητές μπορούν να λάβουν σημαντικές πληροφορίες σχετικά με τη συγχώνευση δυαδικών μαύρων τρυπών που ... ΠερισσότεραΗ αστρονομία των βαρυτικών κυμάτων ακούγεται σαν επιστημονική φαντασία: δύο τεράστιες μαύρες τρύπες στροβιλίζονται η μία προς την άλλη σε ένα σημαντικό κλάσμα της ταχύτητας του φωτός, εκπέμποντας μια έκρηξη ενέργειας που υπερβαίνει τον Ήλιο με τη μορφή βαρυτικών κυμάτων. Εκατομμύρια έτη φωτός μακριά, στη Γη, παρατηρούμε αυτούς τους κυματισμούς στη γεωμετρία του χωροχρόνου μέσω των μικροσκοπικών παραμορφώσεων που παράγουν σε βραχίονες βραχιόνων χιλιομετρικών παρεμβολών [ 1]. Ένα κρίσιμο συστατικό για την ερμηνεία αυτών των σημάτων κύματος βαρύτητας είναι η ακριβής θεωρητική πρόβλεψη για τις παρατηρούμενες κυματομορφές, που λαμβάνονται μέσω της διαβόητα δύσκολης αποστολής επίλυσης των εξισώσεων πεδίου του Αϊνστάιν. Η μελλοντική πρόοδος εξαρτάται από τη σημαντική βελτίωση αυτών των θεωρητικών υπολογισμών, καθώς οι τρέχουσες προβλέψεις ενδέχεται να μην είναι αρκετά ακριβείς για τους αναβαθμισμένους ανιχνευτές που θα συνδεθούν στο διαδίκτυο το 2022 [ 2]. Εμπνευσμένη από τη φυσική των σωματιδίων, όπου τα πάντα είναι εννοιολογικά μειωμένα σε διεργασίες διασποράς μεταξύ σωματιδίων σημείου, ορισμένοι θεωρητικοί έχουν αρχίσει να επιτίθενται στο πρόβλημα των δυαδικών μαύρων τρυπών μελετώντας ένα σχετικό πρόβλημα στο οποίο δύο μαύρες τρύπες πετούν το ένα κοντά στο άλλο και παραμορφώνονται (διασκορπίζονται) από τους βαρυτική αλληλεπίδραση. Σε αυτό το πλαίσιο, ο Thibault Damour από το Ινστιτούτο Προηγμένων Επιστημονικών Σπουδών (IHÉS) στη Γαλλία και συνεργάτες του έχουν προκαλέσει απρόβλεπτη πρόοδο στις θεωρητικές προβλέψεις κύματος βαρύτητας [ 3 - 5 ]. Η τελευταία δουλειά τους δείχνει ότι υπάρχει μια υπολογιστική συντόμευση για το γενικό πρόβλημα σκέδασης, λαμβάνοντας υπόψη ένα ειδικό όριο όπου η μαύρη τρύπα ζυγίζει πολύ λιγότερο από την άλλη.
Η ανίχνευση βαρυτικών κυμάτων - καθώς και η εξαγωγή πληροφοριών πηγής (όπως μάζα, περιστροφή και τοποθεσία) και ο έλεγχος της θεμελιώδους φυσικής - βασίζεται σε μεγάλο βαθμό σε ακριβή θεωρητικά μοντέλα που χρησιμοποιούνται ως πρότυπα στην ανάλυση δεδομένων. Τόσο οι εξελιγμένες αριθμητικές προσομοιώσεις όσο και οι ανασταλτικοί αναλυτικοί υπολογισμοί είναι απαραίτητοι για αυτό το σκοπό και και οι δύο πρέπει να βελτιωθούν με ακρίβεια προκειμένου να αναλυθούν τα δεδομένα που θα προέλθουν από πρόσφατα βελτιωμένα παρατηρητήρια (LIGO, Virgo και KAGRA) και μελλοντικά όργανα (LISA, Cosmic Explorer , και το Τηλεσκόπιο του Αϊνστάιν) [ 2 ].
Στη θεωρία διαταραχών, οι εξισώσεις κίνησης γράφονται ως μια σειρά όρων που περιέχουν κάποια μικρή ποσότητα 𝜖 μεταφερθεί στις αυξανόμενες εξουσίες: πρώτη τάξη 𝜖, δεύτερη παραγγελία 𝜖2, τρίτη παραγγελία 𝜖3, κ.λπ. Το τοπίο των διαταραχών αναλυτικών μεθόδων μπορεί να χαρτογραφηθεί σύμφωνα με την ποσότητα που είναι μικρή: ένα αδύναμο βαρυτικό πεδίο (μετά την επέκταση του Minkowskian), ένα αδύναμο πεδίο και μαύρες τρύπες με αργή κίνηση (μετά την επέκταση του Νεύτωνα) ή μια μικρή αναλογία μάζας μεταξύ των μαύρων οπών (όπως στο πρόγραμμα βαρυτικής αυτο-δύναμης). Στο παρελθόν, η προσέγγιση μετά τον Μινκόφσκιν έλαβε τη λιγότερη προσοχή, καθώς είναι πιο χρήσιμη για τη διασπορά των μαύρων οπών - ένα γεγονός που κανονικά θα παρήγαγε πολύ μικρή βαρυτική ακτινοβολία για να παρατηρηθεί. Ωστόσο, οι θεωρητικοί συνειδητοποίησαν πρόσφατα ότι οι υπολογισμοί που έγιναν για τη διασπορά (μη δεσμευμένων) μαύρων οπών μπορούν να αποκαλύψουν σημαντικά στοιχεία, όπως το δυναμικό βαρύτητας, για συγχώνευση (δεσμευμένων) συστημάτων. Αυτή η σύνδεση έχει φέρει κοντά ερευνητές από τις κοινότητες κλασικής και κβαντικής βαρύτητας,
Η βασική ιδέα σε αυτήν την προσέγγιση σκέδασης είναι να αντιμετωπίζονται οι μαύρες τρύπες ως κβαντικά σωματίδια που αλληλεπιδρούν μέσω της ανταλλαγής βαρυτονίων, με τον ίδιο τρόπο που τα ηλεκτρόνια αλληλεπιδρούν μέσω της ανταλλαγής φωτονίων (Εικ. 1 ). Συνδυάζοντας όλους τους διαφορετικούς τρόπους με τους οποίους αλληλεπιδρούν τα σωματίδια, οι ερευνητές μπορούν να επιτύχουν εξαιρετικά ακριβείς προβλέψεις - όπως αποδεικνύεται από την πειραματική επιβεβαίωση έως και 12 ψηφίων της προβλεπόμενης ανώμαλης μαγνητικής διπόλης ροπής του ηλεκτρονίου [ 6]. Μια κρίσιμη κβαντική ιδέα είναι ότι τα πλάτη σκέδασης, που δίνουν την πιθανότητα για συγκεκριμένες διεργασίες σκέδασης, περιορίζονται έντονα από τις γενικές αρχές (συμμετρίες, τοποθεσία, διατήρηση της πιθανότητας). Αρκετές ομάδες εφαρμόζουν επί του παρόντος αυτές και άλλες ισχυρές τεχνικές από την κβαντική θεωρία πεδίου για να προσδιορίσουν τα πλάτη βαρυτικής σκέδασης μεταξύ «σωματιδίων μαύρης τρύπας». Τα πλάτη είναι κβαντικά παρατηρήσιμα, αλλά οι ερευνητές μπορούν να εξαγάγουν ένα κλασικό μέρος, το οποίο μπορεί να χρησιμοποιηθεί για την κατασκευή προτύπων για την ανάλυση βαρυτικών κυμάτων [ 7 ].
Η Damour ανακάλυψε μια απλή αλλά εκτεταμένη σύνδεση μεταξύ διαφορετικών προσεγγιστικών προσεγγίσεων σε κλασικούς υπολογισμούς σκέδασης μαύρων τρυπών [ 3 ]. Έχει δείξει ότι η μαζική εξάρτηση της κλασικής συνάρτησης γωνίας σκέδασης είναι τέτοια ώστε η συνάρτηση να μπορεί να σταθεροποιηθεί πλήρως σε μια συγκεκριμένη σειρά κατά την μετά-Μινκοβσσιανή προσέγγιση από χαμηλότερες τάξεις στην προσέγγιση αυτο-δύναμης (μικρός-λόγος μάζας). Αυτό το εύρημα είναι ισχυρό αφού η τελευταία προσέγγιση χρησιμοποιεί πλήρως τις ακριβείς (μη γραμμικές) λύσεις μαύρης τρύπας στην κλασική βαρύτητα του Αϊνστάιν. Για παράδειγμα, σύμφωνα με τα ευρήματα του Νταμούρ, η τέταρτη σειρά στην προσέγγιση μετά τον Μινκοβσκόνια - μία σειρά πάνω από τον υπερσύγχρονο υπολογισμό κβαντικού πλάτους που επιτεύχθηκε από τη Zvi Bern και συνεργάτες [ 7] - θα μπορούσε να προσδιοριστεί μόνο από τους υπολογισμούς αυτοβίας πρώτης τάξης. Αυτή η συντόμευση θα μπορούσε να επιταχύνει τις προσπάθειες για την επίτευξη προβλέψεων υψηλότερης τάξης (πιο ακριβείς) στο μέλλον. Ήδη, ο Damour και οι συνάδελφοί του έχουν χρησιμοποιήσει υπολογισμούς αυτοβίας πρώτης τάξεως για να προσδιορίσουν μεγάλα τμήματα της συντηρητικής δυναμικής πέμπτης έως έκτης τάξης, που απαιτούνται για τον προσδιορισμό του δυναμικού βαρύτητας στα δεσμευμένα συστήματα [ 4 , 5 , 8 ]. Μερικοί από τους όρους σε αυτούς τους υπολογισμούς έχουν συζητηθεί έντονα και αποτέλεσαν αντικείμενο φιλικού στοιχήματος μεταξύ της Βέρνης και της Νταμούρ [ 9 ], την οποία δέχτηκε πρόσφατα ο Νταμούρ [ 5 ].
Ενώ η προώθηση των διαταραχών υψηλής τάξης είναι σίγουρα σημαντική, η Damour έχει επίσης προκαλέσει την κοινότητα θέτοντας ζητήματα σχετικά με τις θεμελιώδεις πτυχές της κβαντικής βαρυτικής έρευνας σκέδασης [ 3 ]. Έχει θέσει πολλές λεπτές ερωτήσεις: Έχει νόημα να αναγνωρίσουμε ένα κλασικό μέρος ενός πλάτους σκέδασης, το οποίο είναι συνήθως ένα πιθανό κβαντικό παρατηρούμενο χωρίς άμεσο κλασικό ανάλογο; Πόσο ακριβώς προσθέτει η ανταλλαγή βαρυτών σε μεγάλες κλασικές γωνίες εκτροπής; Πώς σχετίζεται η κλασική σκέδαση της μαύρης τρύπας στο όριο υψηλής ενέργειας με τα κβαντικά αποτελέσματα για τη διασπορά σωματιδίων χωρίς μάζα [ 10 , 11 ]; Η επίλυση αυτών των ζητημάτων θα μπορούσε να βοηθήσει τους ερευνητές να χαρτογραφήσουν μελλοντικούς δρόμους για να κάνουν πιο ακριβείς προβλέψεις.
Η μελέτη της διασποράς των μαύρων τρυπών έχει γίνει μια πολλά υποσχόμενη ερευνητική κατεύθυνση, προσελκύοντας διαφορετικές ομάδες που εργάζονται σε ένα ευρύ φάσμα μεθοδολογιών. Οι πιο πρόσφατες προσπάθειες [ 3 - 5 , 7 , 8 , 12 ] καταδεικνύουν τις δυνατότητες αυτής της προσέγγισης για την επιστήμη των βαρυτικών κυμάτων: Οι ακριβέστερες προβλέψεις σε υψηλές τάξεις στη θεωρία διαταραχών έρχονται προσιτές και η περαιτέρω πρόοδος σε αυτόν τον τομέα μπορεί να βελτιώσει σημαντικά επιστημονική ικανότητα των μελλοντικών παρατηρητηρίων βαρυτικών κυμάτων. Επιπλέον, η αντιπαράθεση διαφορετικών κοινοτήτων και οι τρόποι σκέψης τους φέρουν απρόβλεπτες ευκαιρίες για θεωρητικές ανακαλύψεις, ακόμη και πέρα από τα βαρυτικά κύματα. Ήρθε η ώρα να περάσει αυτός ο ορίζοντας.
Η έρευνα δημοσιεύεται στο περιοδικό Physical Review D .
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Monday, July 20, 2020
Η κβαντική τηλεμεταφορά διαμεσολαβείται από επιφανειακό πλασμόνιο
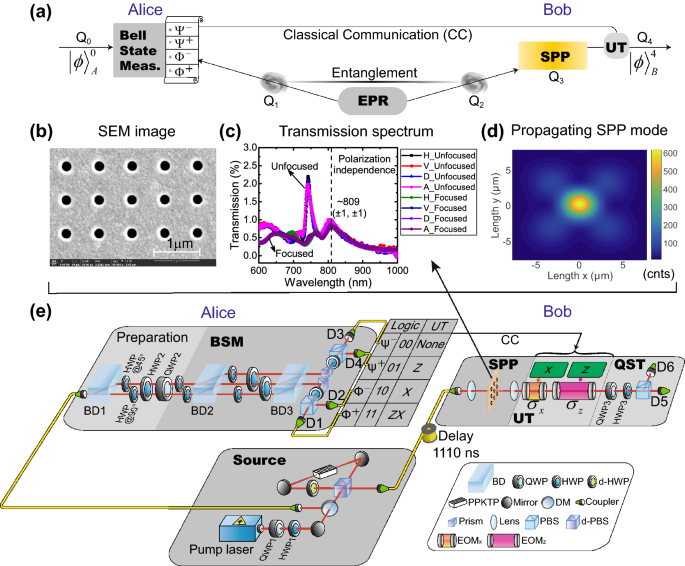
Αφηρημένη Οι polaritons επιφανειακού πλασμονίου (SPPs) είναι συλλογικές διεγέρσεις ελεύθερων ηλεκτρονίων που διαδίδονται κατά μήκος μιας μεταλλικής-διηλεκτρικής διεπαφής. Παρόλο που έχουν δειχθεί κάποιες βασικές κβαντικές ιδιότητες των SPP, όπως η διατήρηση της εμπλοκής, η δυαδικότητα των κυμάτων-σωματιδίων ενός μόνο πλασμώματος, η κβαντική παρεμβολή δύο πλασμίων και η επαλήθευση της δημιουργίας εμπλοκών, έχουν προκύψει ακόμη πιο προηγμένα πρωτόκολλα κβαντικής πληροφορίας για επίδειξη με SPPs. Εδώ, πραγματοποιούμε πειραματικά την τηλεμεταφορά κβαντικής κατάστασης μεταξύ μεμονωμένων φωτονίων και SPPs. Για να το επιτύχουμε αυτό, χρησιμοποιούμε ζεύγη φωτονίων που εμπλέκονται στην πόλωση, συνεκτική μετατροπή φωτονίων-πλασμώματος-φωτονίου σε μια μεταλλική διάταξη οπών υπο-μήκους κύματος, πλήρεις μετρήσεις κατάστασης Bell και μια ενεργή τεχνική προώθησης τροφοδοσίας. Τα αποτελέσματα τόσο της κβαντικής κατάστασης όσο και της κβαντικής τομογραφίας διεργασίας επιβεβαιώνουν την κβαντική φύση της τηλεμεταφοράς μέσω της SPP. Μέση κρατική πιστότηταΕπιτυγχάνονται \ (0,889 \ pm 0,004 \) και μια πιστότητα διεργασίας \ (0,820 \ pm 0,005 \) , που είναι πολύ πάνω από το κλασικό όριο. Η δουλειά μας δείχνει ότι τα SPPs μπορεί να είναι χρήσιμα για την υλοποίηση σύνθετων κβαντικών πρωτοκόλλων σε ένα φωτονικό-πλασμικό υβριδικό κβαντικό δίκτυο. Εισαγωγή Η υβριδική φύση της ελαφριάς ύλης των επιφανειακών πλασμονίων (SPPs) επιτρέπει στο φως να περιορίζεται κάτω από το όριο περίθλασης, ανοίγοντας τη δυνατότητα ολοκλήρωσης φωτονικής συσκευής μήκους κύματος 1 . Οι κβαντικές ιδιότητες των SPPs προέρχονται από κβαντικά επιφανειακά κύματα πλάσματος και πολλά κβαντικά μοντέλα έχουν προταθεί για να περιγράψουν το ηλεκτρομαγνητικό πεδίο ενός πλασμώματος 2 , 3 . Η κβαντοποίηση των SPPs έχει παρακινήσει πολλούς ερευνητές να διερευνήσουν τα θεμελιώδη κβαντικά φαινόμενα που σχετίζονται με αυτά, για παράδειγμα, μετάδοση με εμπλοκή φωτονίων 4 , 5 , δημιουργία και ανίχνευση κατάστασης ενός πλασμώνα 6 , 7, κβαντικές στατιστικές και παρεμβολές στα πλασμικά συστήματα 8 , 9 , 10 , 11 , 12 , 13 , κβαντικές λογικές λειτουργίες 14 , αντι-συγχώνευση των SPPs παρουσία των απωλειών 15 και κβαντική πλασματική κατάσταση N00N για την κβαντική ανίχνευση 16 . Για κριτικές, ανατρέξτε στην Αναφορά 17 , 18 . Πρόσφατα, διερευνήθηκαν επίσης ορισμένες κβαντικές ιδιότητες νέων πλασμικών μετα-υλικών, όπως συνεκτική τέλεια απορρόφηση σε πλασμικά μετα-υλικά με εμπλεγμένα φωτόνια 19 , δοκιμή υπερ-πολύπλοκων κβαντικών θεωριών με αρνητικά διαθλαστικά δείγματα μετα-υλικών 20και τον ενεργό έλεγχο των πλασμικών μετα-υλικών που λειτουργούν στο κβαντικό καθεστώς 21 . Αυτά τα έργα μας παρακινούν να μελετήσουμε και να χρησιμοποιήσουμε τις κβαντικές ιδιότητες των SPP σε πιο προηγμένα πρωτόκολλα κβαντικής πληροφορίας. Η κβαντική τηλεμεταφορά χρησιμοποιεί την εμπλοκή ως πόρο για τη πιστή μεταφορά άγνωστων κβαντικών καταστάσεων μεταξύ απομακρυσμένων κόμβων. Από τότε που παρουσιάστηκε για πρώτη φορά από τους Bennett et al. 22 και πραγματοποιήθηκε πειραματικά χρησιμοποιώντας φωτονικά qubits 23 , 24 , η κβαντική τηλεμεταφορά έχει γίνει το βασικό πρωτόκολλο για τη δημιουργία παγκόσμιων κβαντικών δικτύων 25 , 26 . Η απόσταση τηλεμεταφοράς έχει αυξηθεί σημαντικά τις τελευταίες δύο δεκαετίες 27 , 28 , 29 , 30 , 31και πρόσφατα επεκτάθηκε με επιτυχία σε περισσότερα από χίλια χιλιόμετρα από το έδαφος σε δορυφόρο 32 . Για τη δημιουργία ενός κβαντικού δικτύου με περισσότερες λειτουργίες, απαιτούνται διάφορα φυσικά συστήματα με μεμονωμένα πλεονεκτήματα όσον αφορά τη μεταφορά και την επεξεργασία της κβαντικής κατάστασης. Αποτελέσματα Το εννοιολογικό σχήμα του SPP μεσολαβεί στην κβαντική τηλεμεταφορά Εμείς πειραματικά συνειδητοποιούν την κβαντική κατάσταση τηλεμεταφοράς ενός φωτονίου σε ένα μόνο SPP, το οποίο είναι ένα ενιαίο qubit που αποτελείται από συλλογικών ηλεκτρονικών διεγέρσεων που κατά κανόνα συνεπάγεται ηλεκτρόνια 17 . Το σχέδιό μας βασίζεται σε τρία qubit, το οποίο προτάθηκε για πρώτη φορά από τον Popescu 33 και υλοποιήθηκε σε πείραμα από τους Boshi et al. 24 . Το εννοιολογικό πλαίσιο του πειράματός μας με το σχήμα τριών qubit φαίνεται στο σχήμα 1 α. Η εμπλοκή μεταξύ των qubits 1 (Q1) και 2 (Q2), που χρησιμεύει ως κβαντικό κανάλι, δημιουργείται από την πηγή των εμπλεκόμενων ζευγών φωτονίων και διανέμεται στην Alice και τον Bob. Μια κατάσταση εισαγωγής του qubit 0 (Q0) αποστέλλεται στην Alice. Η Αλίκη εκτελεί μέτρηση κατάστασης Bell (BSM) 24 ∼ 10 6 , προβάλλοντας Q0 και Q1 τυχαία σε μία από τις τέσσερις καταστάσεις Bell, η καθεμία με πιθανότητα 25%. Στη συνέχεια, τα αποτελέσματα του BSM αποστέλλονται στον Bob μέσω ενός καναλιού κλασικής επικοινωνίας (CC). Το Q2 αποστέλλεται σε ένα δείγμα συστοιχίας τρύπας μήκους κύματος με σχέδιο σε μια χρυσή μεμβράνη στην τοποθεσία του Bob για τη διευκόλυνση της μετατροπής φωτονίου-SPP-φωτονίου 34 . Εκεί, η κβαντική κατάσταση του Q2 μεταφέρεται στο qubit 3 (Q3), που μεταφέρεται από ένα μόνο SPP. Αυτό το SPP διαδίδεται κατά μήκος της επιφάνειας του δείγματος και στη συνέχεια συνδέεται με ένα οπτικό φωτόνιο (Q4), το οποίο ακτινοβολεί προς ανιχνευτές στο μακρινό πεδίο. Σύμφωνα με τα αποτελέσματα του BSM, οι αντίστοιχοι ενιαίοι μετασχηματισμοί (UTs) εφαρμόζονται στο Q4. Τέλος, εκτελούμε τομογραφία κβαντικής κατάστασης (QST) 35 , 36 στο Q4 και επαληθεύστε εάν η τηλεμεταφορά κβαντικής κατάστασης από ένα μόνο φωτόνιο σε ένα SPP είναι επιτυχής αξιολογώντας την πιστότητα της κβαντικής κατάστασης από Q4 έως Q0 και την πιστότητα της κβαντικής διαδικασίας ολόκληρης της διαδικασίας. Διάταξη οπών υποβρύχιου μήκους και χαρακτηρισμός της Το Σχήμα 1 b δείχνει μια εικόνα μικροσκοπίας ηλεκτρονικής σάρωσης (SEM) της συστοιχίας οπών μήκους κύματος που χρησιμοποιείται στο πείραμά μας. Το χρυσό φιλμ είναι διάτρητο σε μια τετραγωνική περιοχή με περιοδικές συστοιχίες οπών χρησιμοποιώντας μια εστιασμένη δέσμη ιόντων. Η διάμετρος της οπής και η περίοδος είναι 200 nm και 700 nm, αντίστοιχα. Το πάχος της μεταλλικής μεμβράνης μας είναι 150-nm. Παρόλο που η συστοιχία οπών μειώνει την άμεση μετάδοση φωτονίων, επιτρέπει τη διέγερση συντονισμού του SPP 34 . 189 × 189 μ Μ 2 Το φάσμα μετάδοσης του δείγματος μας φαίνεται στο Σχ. 1 c και έχει μια κορυφή κεντραρισμένη στα 809 nm περίπου με πλήρες πλάτος στο μισό μέγιστο (FWHM) . Η μέγιστη μετάδοση του δείγματος στα 809 nm είναι περίπου 0,8%. Η εξαιρετική οπτική μετάδοση (EOT) που παρατηρείται στις συστοιχίες οπών υποβρύχιου μήκους κύματος είναι ένα τυπικό φαινόμενο συντονισμού συντονισμού που προκύπτει από την εποικοδομητική παρεμβολή όταν τα φωτόνια διέρχονται από τις οπές 34 , 37 . Σε σύγκριση με άλλα έργα 4 , 34 , η συνολική μετάδοση του δείγματος μας είναι ελαφρώς χαμηλότερη. Ο λόγος είναι ότι το φάσμα μετάδοσης είναι πολύ ευαίσθητο στις γεωμετρικές παραμέτρους του συστήματος 37 ∼ 70 νμ , 38 . Οι ατέλειες κατά τη διάρκεια της κατασκευής μπορούν να οδηγήσουν στο σχήμα της οπής, στην περίοδο του πλέγματος καθώς και στο πάχος και την ομαλότητα του χρυσού φιλμ που απομακρύνεται από τις ονομαστικές ρυθμίσεις, με αποτέλεσμα την χαμηλή μετάδοση 39 . Ακόμη και ο καθορισμός των ίδιων παραμέτρων, η μετάδοση δειγμάτων που κατασκευάστηκαν σε διαφορετικούς χρόνους έχει κάποιες εμφανείς διαφορές και είναι χαμηλότερη από 3% λόγω των ατελειών κατασκευής 4 . Ωστόσο, χρησιμοποιούμε μόνο τις πληροφορίες συχνότητας, δηλαδή τη θέση αιχμής, αντί της μετάδοσης στο πείραμα τηλεμεταφοράς μας. Αν και η συνολική μας μετάδοση είναι μικρότερη από 2,5%, είναι ακόμη μεγαλύτερη από την τιμή που προβλέπει η τυπική θεωρία διαφράγματος 34, που δείχνει ότι ο ΕΟΤ συμβαίνει στο δείγμα μας. Οι καμπύλες μετάδοσης για διαφορετικές πόλωση φωτός είναι παρόμοιες, υποδηλώνοντας ότι το δείγμα μας είναι σχεδόν ανεξάρτητο από πόλωση. Η μη ευαισθησία πόλωσης οφείλεται στη συμμετρία του τετραγωνικού δικτυωτού πλέγματος, όπως έχει αποδειχθεί σε προηγούμενα έργα 38 , 40 , 41 . Ένας αριθμητικός υπολογισμός που βασίζεται στη γεωμετρία της συστοιχίας και στην αντιστοίχιση των κυμάτων κυμάτων δείχνει ότι αυτή η κορυφή συνδέεται με τις λειτουργίες SPP ( ) στη διεπαφή γυαλιού-μετάλλου 42 . Αυτοί οι τρόποι μπορούν να διεγείρουν τα SPP που διαδίδονται κατά μήκος των τεσσάρων διαγώνιων κατευθύνσεων. Μετράμε πειραματικά τη διάδοση του SPP με ένα λέιζερ και μια συσκευή συζευγμένης φόρτισης (CCD), όπως φαίνεται στο Σχ. ± 1 , ± 1 1 δ. Εφαρμόζοντας τη διάδοση SPP κατά μήκος της διαγώνιας κατεύθυνσης, εκτιμούμε ότι το μήκος αποσύνθεσης 1 / e της πλασματικής λειτουργίας είναι . Ανατρέξτε στις Συμπληρωματικές πληροφορίες για περισσότερες λεπτομέρειες σχετικά με την αριθμητική προσομοίωση, το σχεδιασμό της διάταξης οπών και τους χαρακτηρισμούς αυτής της συσκευής. ∼ 4.48 ± 0,50 μ Μ Πραγματοποίηση κβαντικής τηλεμεταφοράς μεταξύ φωτονίου και SPP Το σχήμα 1 ε παρουσιάζει μια διάταξη της πειραματικής μας ρύθμισης. Τα εμπλεκόμενα ζεύγη φωτονίων δημιουργούνται από αυθόρμητη παραμετρική μετατροπή προς τα κάτω, η οποία πραγματοποιείται ενσωματώνοντας έναν περιοδικά πολωμένο κρύσταλλο (PPKTP) σε ένα παρεμβολόμετρο Sagnac 43 , 44 . Η κβαντική κατάσταση των φωτονίων Α και Β είναι παρόμοια με την απλή κατάσταση: KTiOPO 4 | Ψ - ⟩ ΕΝΑ σι = 1 √ 2 ( | Η ⟩ ΕΝΑ | Β ⟩ σι - | Β ⟩ ΕΝΑ | Η ⟩ σι ) , (1) που έχει πιστότητα περίπου . ( ) υποδηλώνει την οριζόντια (κατακόρυφη) κατάσταση πόλωσης του φωτονίου A. Η ίδια σημείωση χρησιμοποιείται για το φωτονίο Β. Λαμβάνουμε σύμπτωση μετρά με ρυθμό περίπου 100 kHz με ισχύ αντλίας 20 mW. 98 % | Η ⟩ ΕΝΑ | Β ⟩ Φιγούρα Φιγούρα 1
Η πειραματική διάταξη της επιφανειακής πλασμόνης polariton (SPP) μεσολαβεί στην κβαντική τηλεμεταφορά. ( α ) Το εννοιολογικό πλαίσιο του πειράματός μας. Στον ιστότοπο της Alice, οι καταστάσεις εισαγωγής προετοιμάζονται χρησιμοποιώντας το qubit 0 (Q0). Μια πηγή Einstein-Podolsky-Rosen (EPR) παράγει δύο εμπλεγμένα qubits, Q1 και Q2. Το Q1 αποστέλλεται στην Alice για μέτρηση κατάστασης Bell (BSM) 24 . Το Q2 αποστέλλεται στον Bob για να διεγείρει το SPP qubit, Q3. Μέσω της μετατροπής φωτονίου-πλασμώνα-φωτονίου, οι κβαντικές καταστάσεις των SPP μετατρέπονται πίσω σε ένα φωτονικό qubit, Q4. Τα αποτελέσματα του BSM αποστέλλονται στον Bob χρησιμοποιώντας την κλασική επικοινωνία (CC). Ο Μπομπ τότε εφαρμόζει έναν ενιαίο μετασχηματισμό (UT) στο Q4. Ως αποτέλεσμα, η κατάσταση εξόδου είναι ίδια με το | ϕ ⟩ σι 4 | ϕ ⟩ ΕΝΑ 0 ; Ως εκ τούτου, η τηλεμεταφορά επιτυγχάνεται. ( β ) Η εικόνα SEM των συστοιχιών οπών υπογευμάτων με διάμετρο 200 nm και περίοδο 700 nm ( γ ) Φάσμα μετάδοσης των συστοιχιών οπών. Ο συντονισμός στα 809 nm περίπου (διακεκομμένη γραμμή) είναι η λειτουργία ( , ), που αντιστοιχεί στα SPP που διαδίδονται κατά τη διαγώνια κατεύθυνση. ( δ ) Η εικόνα του πεδίου δείχνει τη λειτουργία διάδοσης SPP. Οι μονάδες «μετρά» (cnts) επισημαίνονται κάτω από τη γραμμή χρωμάτων. ( ε ) Σκίτσο της πειραματικής ρύθμισης. Η πηγή που έχει εμπλακεί στην πόλωση χρησιμοποιεί ένα συμβολόμετρο Sagnac προς τα κάτω μετατροπής τύπου II, όπου ένα μη γραμμικό κρύσταλλο\ pm 1 \ pm 1 \ chi ^ {(2)} \ hbox {KTiOPO} _4 \ sigma _x \ sigma _z I, \ sigma _z, \ sigma _x, εγώ σίγμα ± 1 ± 1 χ ( 2 ) KTiOPO 4 , PPKTP) αντλείται συνεκτικά από φως λέιζερ 405 nm από δεξιόστροφα και αριστερόστροφα. Το κεντρικό μήκος κύματος των εμπλεγμένων φωτονίων σήματος (Α) και ρελαντί (Β) είναι περίπου 810 nm. Το Photon A αποστέλλεται στην Alice. Ο βαθμός πόλωσης της ελευθερίας (DOF) (Q0) του φωτονίου Α χρησιμοποιείται για την προετοιμασία των έξι καταστάσεων εισόδου. Οι τέσσερις καταστάσεις καμπάνας κατασκευάζονται χρησιμοποιώντας τη διαδρομή (Q1) και την πόλωση (Q0) DOF του φωτονίου A. Το φωτον Β αποστέλλεται στον Μπομπ. Η πόλωση του φωτονίου Β (Q2) χρησιμοποιείται για να διεγείρει τα SPPs. Αφού υποβληθεί σε μετατροπή φωτονίου-πλασμώνα-φωτονίου, η κβαντική κατάσταση των SPPs (Q3) μεταφέρεται πίσω στο φωτόνιο (Q4). Τα αποτελέσματα του BSM (00, 01, 10, 11) αποστέλλονται στον Bob από τον CC και στη συνέχεια χρησιμοποιούνται για την ενεργοποίηση των ηλεκτρο-οπτικών διαμορφωτών (EOM, , σ Χ σ ζ ) για να εφαρμόσετε τα αντίστοιχα UT ( ). Η κβαντική κατάσταση αναλύεται τελικά μέσω κβαντικής τομογραφίας (QST). HWP: πλάκα μισού κύματος. QWP: πλάκα τετάρτου κύματος. BD: μετατοπιστής δέσμης; DM: διχρωμικός καθρέφτης d-PBS: διαχωριστής πολωτικής δέσμης διπλού μήκους κύματος. Εγώ , σ ζ , σ Χ , Εγώ σ Σχήμα 2 Σχήμα Σχήμα 2
Ανακατασκευασμένοι πίνακες πυκνότητας των έξι καταστάσεων με τηλεμεταφορά. ( α ) Οι αρχικές προετοιμασμένες καταστάσεις είναι , , , , , και και υποδεικνύονται με χρωματιστές κουκκίδες στη σφαίρα Bloch. ( b , d , f , h , j , l ) Πραγματικά μέρη των πινάκων πυκνότητας που ανακατασκευάστηκαν για τις έξι καταστάσεις. ( c , e , g , i , k , m | Η ⟩ | Β ⟩ | ρε ⟩ | ΕΝΑ ⟩ | Ρ ⟩ | μεγάλο ⟩ ) Φανταστικά μέρη των πινάκων ανακατασκευασμένης πυκνότητας για τις έξι καταστάσεις. Η ιδανική μήτρα πυκνότητας εμφανίζεται ως το πλέγμα καλωδίων. Τα αντιπροσωπευτικά δεδομένα εδώ είναι για πειράματα με ένα αποτέλεσμα μέτρησης Bell-state με SPP. Οι ανακατασκευασμένοι πίνακες πυκνότητας των έξι καταστάσεων και για τα τέσσερα αποτελέσματα μέτρησης της κατάστασης Bell παρέχονται στις Συμπληρωματικές Πληροφορίες. | Φ + ⟩
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Tuesday, July 14, 2020
Κβαντικό πείραμα διπλής σχισμής με φωτόνια εμπλεγμένα με ορμή
Το πείραμα σκέψης διπλής σχισμής παρέχει βαθιά εικόνα για την παρέμβαση των κβαντικών σωματιδίων. Αυτή η εργασία παρουσιάζει μια λεπτομερή πειραματική πραγματοποίηση του πειράματος κβαντικής σκέψης διπλής σχισμής με φωτόνια που έχουν εμπλακεί σε ορμή και θεωρητική ανάλυση του πειράματος. Το πείραμα διαμορφώνεται με τέτοιο τρόπο ώστε τα φωτόνια να εμπλέκονται στη διαδρομή και κάθε φωτόνιο να μπορεί να αποκαλύψει τις πληροφορίες πορείας της άλλης φωτονίδας. Κατά συνέπεια, η παρεμβολή ενός φωτονίου καταστέλλεται. Ωστόσο, το μοτίβο παρεμβολών δύο φωτονίων εμφανίζεται εάν οι θέσεις ανίχνευσης των φωτονίων συσχετίζονται χωρίς να αποκαλύπτονται οι πληροφορίες πορείας ποιας σχισμής. Αποδεικνύεται επίσης πειραματικά και θεωρητικά ότι η κβαντική παρεμβολή δύο φωτονίων εξαφανίζεται όταν ανιχνεύεται η πορεία κοπής ενός φωτονίου στη διπλή σχισμή. Εισαγωγή Η κυματική φύση του φωτός αποδείχθηκε αρχικά πειραματικά με το πείραμα 1 , 2 του διάσημου Young . Στην κβαντική φυσική, το φως κβαντοποιείται με τη μορφή κβαντικής ενέργειας γνωστής ως φωτονίου. Σύμφωνα με τη δήλωση του PAM Dirac, «Κάθε φωτονίο παρεμβαίνει μόνο στον εαυτό του» 3 . Αυτή η μόνη παρέμβαση ενός φωτονίου είναι συνέπεια της αρχής της κβαντικής υπέρθεσης. Εάν τα φωτόνια εμφανίζονται σε μια διπλή σχισμή ένα προς ένα, τότε το μοτίβο παρεμβολής ενός φωτονίου εμφανίζεται σταδιακά. Όπου η ανίχνευση κάθε φωτονίου αντιστοιχεί σε ένα σημείο στην οθόνη. Το πείραμα Double-slit του Young παρέχει βαθιά εικόνα για τη δυαδικότητα των κυμάτων-σωματιδίων εάν είναι φανταστικό για μεμονωμένα σωματίδια 4. Το μοτίβο παρεμβολής ενός μεμονωμένου σωματιδίου δεν σχηματίζεται εάν είναι γνωστές οι πληροφορίες διαδρομής ενός σωματιδίου, δηλαδή μια σχισμή μέσω της οποίας έχει περάσει ένα σωματίδιο. Σύμφωνα με την ερμηνεία της Κοπεγχάγης, μια παρατήρηση σχετικά με την κβαντική υπέρθεση των διαδρομών ενός σωματιδίου αντιστοιχεί σε μια μέτρηση που καταρρέει την κβαντική υπέρθεση, επομένως, δεν σχηματίζεται μοτίβο παρεμβολών. Από την άλλη πλευρά, τι συμβαίνει εάν τροποποιήσουμε το πείραμα με τέτοιο τρόπο ώστε οι πληροφορίες πορείας ενός σωματιδίου να μην είναι διαθέσιμες κατά τη διέλευσή του μέσω διπλής σχισμής, αλλά μπορούν να ληφθούν ακόμη και μετά την ανίχνευσή του. Σε αυτήν την περίπτωση, η πορεία πορείας μπορεί να πραγματοποιηθεί από την κβαντική κατάσταση ενός άλλου σωματιδίου εάν η συνολική κβαντική κατάσταση των σωματιδίων είναι μια εμπλεγμένη κβαντική κατάσταση. Γνωρίζοντας την πορεία του με μια μέτρηση, προσδιορίζεται αμέσως η πληροφορία διαδρομής του άλλου σωματιδίου. Λόγω της διαδρομής που αποκαλύπτει την κβαντική εμπλοκή των σωματιδίων, καταστέλλεται η παρεμβολή μεμονωμένων σωματιδίων. Ωστόσο, η κβαντική παρεμβολή μπορεί να ανακτηθεί ακόμα και μετά την ολοκλήρωση του πειράματος κάνοντας συσχετισμένη επιλογή των αποτελεσμάτων της μέτρησης. Το πρώτο πείραμα που έδειξε την παρεμβολή του φωτός με πολύ χαμηλή ένταση στο πείραμα Young-double-slit πραγματοποιήθηκε το 1909 από τον GI Taylor 5 . Ενδιαφέροντα πειράματα που δείχνουν τις παρεμβολές διπλής σχισμής του Young εκτελούνται με νετρόνια από τη θεμελιώδη προοπτική της κβαντικής μηχανικής 6 , με δέσμες ηλεκτρονίων 7 και με ένα μόνο ηλεκτρόνιο που διέρχεται από μια διπλή σχισμή 8 , 9 , 10 . Πρόσφατα, αναφέρθηκε μια πρώτη πειραματική επίδειξη παρεμβολής αντισωμάτων με διπλή σχισμή 11 . Η παρέμβαση των μακρομορίων είναι το αντικείμενο μεγάλου ενδιαφέροντος για την αναζήτηση της κβαντικής υπέρθεσης μεσοσκοπικών και μακροσκοπικών αντικειμένων12 , 13 . Σε αυτό το πλαίσιο, έχουν πραγματοποιηθεί πολλά ενδιαφέροντα πειράματα για να παραχθεί μια υπέρθεση διαδρομής μεγάλων μορίων παρόμοια με τα πειράματα παρεμβολής τύπου διπλής σχισμής 14 , 15 , 16 . Η κύρια ιδέα ενός πειράματος κβαντικής μονής διπλής σχισμής επεκτάθηκε σε ένα κβαντικό πείραμα διπλής σχισμής με σκέψη Greenberger, Horne και Zeilinger 17 για να παρέχει θεμελιώδη εικόνα σχετικά με την κβαντική παρέμβαση πολλαπλών σωματιδίων. Στο χαρτί τους. έχουν εξετάσει δύο διπλές σχισμές και μια πηγή σωματιδίων που τοποθετούνται στη μέση των διπλών σχισμών. Κάθε σωματίδιο ανιχνεύεται ξεχωριστά αφού διασχίζει μια διπλή σχισμή. Η κβαντική εμπλοκή σωματιδίων εμφανίζεται φυσικά στις εκτιμήσεις τους 18 , 19και φαίνεται, όταν εξαφανίζονται οι παρεμβολές ενός μορίου και εμφανίζονται δύο παρεμβολές. Μια πειραματική πραγματοποίηση κβαντικού πειράματος με διπλή σχισμή που δείχνει παρεμβολή δύο φωτονίων έχει αποδειχθεί με κβαντικά συσχετισμένα φωτόνια που παράγονται με διαδικασία αυθόρμητης παραμετρικής μετατροπής (SPDC) 20. Ωστόσο, σε αυτό το άρθρο, παρουσιάζουμε μια λεπτομερή πειραματική πραγματοποίηση του πειράματος κβαντικής σκέψης διπλής σχισμής με ζεύγη φωτονίων που έχουν εμπλακεί σε ορμή, όπου πραγματοποιείται μια εικονική διαμόρφωση διπλής σχισμής με δύο διπρισμούς Fresnel. Αυτή η εργασία παρέχει μια λεπτομερή εννοιολογική, θεωρητική και πειραματική ανάλυση του κβαντικού πειράματος διπλής σχισμής. Επιπλέον, παρουσιάζεται ένα πείραμα ανίχνευσης πορείας πορείας φωτονίου όπου αποδεικνύεται ότι η παρεμβολή δύο φωτονίων εξαφανίζεται όταν ανιχνεύεται πορεία κοπής φωτονίου. Σε αυτό το άρθρο, τα πειράματα παρουσιάζονται στο πλαίσιο ενός πειράματος κβαντικής σκέψης διπλής σχισμής. Εντούτοις, μελετήθηκαν εντατικά πειράματα θεμελιώδους σημασίας με τα εμπλεκόμενα στην πόλωση φωτονία 21 , 22 , 23 και τα ορμονικά εμπλεκόμενα φωτόνια 24 . Επιπλέον, ενδιαφέροντα πειράματα σχετικά με τη διαγραφή καθυστερημένης επιλογής διαδρομής 25 , 26 , 27 , 28 , 29 , 30 και παρεμβολών δύο φωτονίων 31 , 32 , 33 , 34 , 35 , 36 , 37 ,Πραγματοποιούνται 38 , 39 , 40 . Παρόμοια πειράματα έχουν προταθεί με το Einstein – Podolsky – Rosen (EPR) εμπλεγμένο ζευγάρι ατόμων 41 .>>>>>>Κβαντικό πείραμα διπλής σχισμήςο κβαντικό πείραμα διπλής σχισμής αποτελείται από δύο διπλές σχισμές και μια πηγή ζευγών φωτονίων. Σε αυτήν την πειραματική κατάσταση, ένα μόνο φωτόνιο διέρχεται από κάθε διπλή σχισμή και ανιχνεύεται ξεχωριστά σε οθόνες τοποθετημένες πίσω από τις διπλές σχισμές, όπως φαίνεται στο Σχ. 1 . Ωστόσο, η παρέμβαση των φωτονίων εξαρτάται από την κβαντική κατάσταση των δύο φωτονίων. Για να κατανοήσετε την κβαντική παρεμβολή δύο φωτονίων σε ένα πείραμα με διπλή σχισμή, λάβετε υπόψη ότι μια πηγή παράγει φωτόνια σε ζεύγη και και τα δύο φωτόνια έχουν την ίδια γραμμική πόλωση. Η διπλή σχισμή 1 και η διπλή σχισμή 2 ευθυγραμμίζονται παράλληλα με τον άξονα y και τοποθετούνται σε αποστάσεις και , αντίστοιχα κατά μήκος του άξονα x από την πηγή. Μονές σχισμές μεγάλο 1 μεγάλο 2 a_ {1} b_ {1} D_ {1} a_ {2} b_ {2} D_ {2} s_ {1} s_ {2} o_ {1} o_ {2} a_ { 1} a_ {2} b_ {1} b_ {2} a_ {1} b_ {2} b_ {1} a_ {2} a_ {12} o_ {1} o_ {2} ένα 1 και της διπλής σχισμής 1 διαχωρίζονται με απόσταση και μεμονωμένες σχισμές και της διπλής σχισμής 2 διαχωρίζεται με απόσταση όπως φαίνεται στο Σχ. 1 όπου κάθε πλάτος σχισμής θεωρείται ότι είναι άπειρα μικρό. Στην οθόνη 1 ανιχνεύεται ένα μοναδικό φωτόνιο ζεύγους φωτονίων, το οποίο είναι τοποθετημένο σε απόσταση από τη διπλή σχισμή 1 και ένα δεύτερο φωτόνιο ανιχνεύεται στην οθόνη 2, η οποία βρίσκεται σε απόσταση από διπλή σχισμή 2. Υπάρχουν τέσσερις διαφορετικές πιθανές διαδρομές με τις οποίες μπορούν να φτάσουν τα φωτόνια στις αντίστοιχες οθόνες, δηλαδή ένα φωτόνιο μπορεί να φτάσει σε ένα σημείο σι 1 ρε 1 ένα 2 σι 2 ρε 2 μικρό 1 μικρό 2 ο 1 στην οθόνη 1 μέσω διπλής σχισμής 1 και το άλλο φωτόνιο μπορεί να φτάσει σε ένα σημείο στην οθόνη 2 μέσω διπλής σχισμής 2. Επομένως, πιθανές διαδρομές φωτονίων είναι ( i) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (ii) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (iii) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (iv) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ο 2 ένα 1 ένα 2 σι 1 σι 2 ένα 1 σι 2 σι 1 ένα 2 . Δεδομένου ότι όλες οι πιθανές διαδρομές δεν είναι διακριτές και δεν αποκαλύπτουν πληροφορίες πορείας, επομένως, συνολικό πλάτος για να βρείτε ένα φωτόνιο στο και ένα φωτόνιο στο μαζί είναι μια κβαντική υπέρθεση όλων των πιθανών διαδρομών, οι οποίες μπορούν να γραφτούν διαδοχικά ως ΕΝΑ 12 ο 1 ο 2 ΕΝΑ 12 = ⟨ ο 2 | ένα 2 ⟩ τ ένα 2 ⟨ ένα 2 | ⟨ ο 1 | ένα 1 ⟩ τ ένα 1 ⟨ ένα 1 | ψ ⟩ + ⟨ ο 2 | σι 2 ⟩ τ σι 2 ⟨ σι 2 | ⟨ ο 1 | σι 1 ⟩ τ σι 1 ⟨ σι 1 | ψ ⟩ + ⟨ ο 2 | σι 2 ⟩ τ σι 2 ⟨ σι 2 | ⟨ ο 1 | ένα 1 ⟩ τ ένα 1 ⟨ ένα 1 | ψ ⟩ + ⟨ ο 2 | ένα 2 ⟩ τ ένα 2 ⟨ ένα 2 | ⟨ ο 1 | σι 1 ⟩ τ σι 1 ⟨ σι 1 | ψ ⟩ (1) όπου , , , είναι πλάτη μετάδοσης σχισμών , , , , αντίστοιχα. Οι κβαντικές καταστάσεις , , είναι θέση διαστημικές βάσεις καταστάσεις θέσεων στις σχισμές σε διπλή σχισμή 1 και διπλή σχισμή 2, αντίστοιχα όπου μπορεί να βρεθεί ένα φωτόνιο Ομοίως, και τ ένα 1 τ σι 1 τ ένα 2 τ σι 2 ένα 1 σι 1 ένα 2 σι 2 | ένα 1 ⟩ | σι 1 ⟩ | ένα 2 ⟩ | σι 2 ⟩ | ο 1 ⟩ | ο 2 ⟩ είναι οι καταστάσεις βάσης θέσης θέσης των τοποθεσιών στις οθόνες. Ωστόσο, οι καταστάσεις βάσης θέσης που αντιστοιχούν σε σημεία σε κάθε διπλή σχισμή και μια οθόνη σχηματίζουν ένα διαφορετικό σύνολο βάσεων έτσι ώστε αντιπροσωπεύει το πλάτος του μεταδιδόμενου φωτονίου που πηγαίνει από τη σχισμή σε μια τοποθεσία στην οθόνη 1. Η ίδια ορολογία εφαρμόζεται για άλλα πλάτη στην Εξ. 1 . ⟨ ο 1 | ένα 1 ⟩ ένα 1 ο 1 Φιγούρα
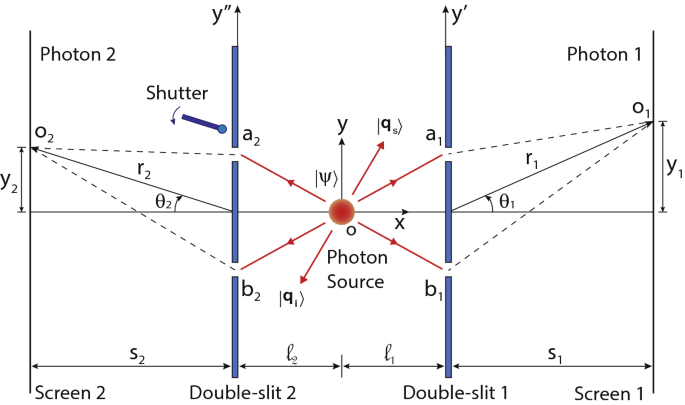
Ένα σχηματικό διάγραμμα ενός πειράματος με διπλή σχισμή. Τα φωτόνια ανιχνεύονται ξεχωριστά σε οθόνες αφού περάσουν ξεχωριστά από τις διπλές σχισμές. Πληροφορίες πορείας πορείας με σχισμή των φωτονίων μπορούν να ανιχνευθούν αποκλείοντας οποιαδήποτε μεμονωμένη σχισμή κλείνοντας το κλείστροΠεραιτέρω, θεωρήστε ότι τα ζεύγη φωτονίων που παράγονται από μια πηγή πεπερασμένου μεγέθους εκπέμπονται σε αντίθετες κατευθύνσεις μεταξύ τους έτσι ώστε να εμπλέκονται η ορμή, η καθαρή ορμή τους είναι μηδέν και η ορμή κάθε φωτονίου είναι σίγουρα άγνωστη. Λάβετε υπόψη ότι η χωρική επέκταση της πηγής είναι πολύ μικρότερη από τον διαχωρισμό των σχισμών, αλλά είναι μεγάλη για την παραγωγή ορμής εμπλοκής. Ως συνέπεια της εμπλοκής της ορμής, εάν ένα φωτόνιο διέρχεται από σχισμή τότε το άλλο φωτόνιο διέρχεται από σχισμή και εάν ένα φωτόνιο διέρχεται από σχισμή έπειτα το άλλο φωτόνιο περνάει από τη σχισμή ένα 1 σι 2 σι 1 ένα 2 μετά τη μετάδοσή τους μέσω των σχισμών. Για τα φωτόνια που εμπλέκονται στην ορμή, και οι δύο αυτές δυνατότητες είναι κβαντικές υπερτιθέμενες, με αποτέλεσμα και τα δύο φωτόνια να εμπλέκονται στη διαδρομή μέσω των σχισμών και των δύο πρώτων όρων στην άθροιση του Εξ. 1 γίνεται μηδέν. Οι δύο τελευταίοι όροι στο άθροισμα οφείλονται στην εμπλοκή της διαδρομής μέσω των σχισμών, αυτά τα δύο πλάτη αλληλεπιδρούν μεταξύ τους και παράγουν παρεμβολή δύο-φωτονίων των εμπλεκόμενων με ορμή φωτονίων. Όταν ανοίγουν και οι τέσσερις σχισμές, δεν αποκαλύπτονται πληροφορίες διαδρομής δύο φωτονίων και μπορεί να παρατηρηθεί παρεμβολή δύο φωτονίων με καταγραφή θέσεων ανίχνευσης ενός φωτονίου που αντιστοιχεί σε μια συγκεκριμένη θέση ανίχνευσης άλλου φωτονίου στην άλλη οθόνη κατά τη διάρκεια κάθε επανάληψης το πείραμα. Από την άλλη πλευρά, εάν κάποιος μετρήσει την κατεύθυνση της ορμής οποιουδήποτε μεμονωμένου φωτονίου πριν από τη διέλευση του μέσω διπλών σχισμών, τότε η κατάσταση εμπλοκής της ορμής καταρρέει. Αυτό το αποτέλεσμα της μέτρησης αποκαλύπτει την κατεύθυνση ορμής ενός φωτονίου στο οποίο πραγματοποιείται μια μέτρηση και η κατεύθυνση της ορμής του άλλου φωτονίου αποκαλύπτεται επίσης αμέσως μετά την κατάρρευση ακόμη και χωρίς να γίνει καμία μέτρηση σε αυτό. Αυτή η μέτρηση αποκαλύπτει ποια διαδρομή διαδρομής των φωτονίων. Από την άλλη πλευρά, ποια διαδρομή σχισμών των φωτονίων στη διπλή σχισμή μπορεί να ανιχνευθεί κλείνοντας οποιαδήποτε μεμονωμένη σχισμή με κλείστρο. Ένα κλείστρο που φαίνεται στο Σχ. 1 θεωρείται ανιχνευτής μέτρησης φωτονίων, εάν το κλείστρο είναι κλειστό για να μπλοκάρει μια σχισμή ένα 2 και ένα φωτόνιο ανιχνεύεται στην οθόνη 2 και στη συνέχεια αποκαλύπτει ότι ένα φωτόνιο περνάει από μια σχισμή λόγω της κατάρρευσης της κβαντικής εμπλοκής κατάστασης που προκαλείται από τον ανιχνευτή κλείστρου. Κατά συνέπεια, μπορεί κανείς να ανακαλύψει ότι το άλλο φωτόνιο περνάει από μια σχισμή εάν εντοπιστεί στο σι 2 ένα 1 ο 1 . Δεδομένου ότι είναι γνωστή μια διαδρομή και των δύο φωτονίων, η παρεμβολή δύο φωτονίων καταστέλλεται. Ενδιαφέρουσα κατάσταση εμφανίζεται όταν οι διπλές σχισμές 2 και η οθόνη 2 αφαιρούνται για να επιτρέψουν σε ένα φωτόνιο να διαδίδεται στο διάστημα ενώ άλλο φωτονίο περνά μέσω της διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1. Μια παρέμβαση ενός φωτονίου δεν παράγεται στην οθόνη 1 λόγω διαδρομής εμπλοκή της πορείας πορείας των φωτονίων μπορεί να ληφθεί μετρώντας την ορμή του φωτονίου διάδοσης ακόμη και μετά την ανίχνευση ενός φωτονίου στην οθόνη 1. Επιπλέον, όταν ανοίγονται όλες οι σχισμές και δεν εντοπίζεται ποια σχισμή, ένα φωτόνιο μπορεί να ανιχνευθεί σε οποιαδήποτε θέση σε μια οθόνη τυχαία κατά τη διάρκεια κάθε επανάληψης του πειράματος και η θέση ανίχνευσής του δεν είναι γνωστή πριν από μια μέτρηση στην οθόνη. Μόλις ένα φωτονίο ανιχνευθεί σε μια οθόνη, η θέση ανίχνευσής του καθορίζει αμέσως το πλάτος για να βρει άλλο φωτονίο σε άλλη οθόνη εάν δεν επιτευχθεί εκεί. Τα μεμονωμένα φωτόνια δεν εμφανίζουν παρεμβολές στην οθόνη επειδή ένα καλά καθορισμένο εύρος συνεκτικής φάσης για την εύρεση ενός φωτονίου στην οθόνη εξαρτάται από μια συγκεκριμένη θέση ανίχνευσης άλλων φωτονίων. Σε αυτήν την περίπτωση, ένα πλάτος ενός φωτονίου είναι εντελώς ασυνεπές. Οι πληροφορίες για τη θέση ανίχνευσης ενός φωτονίου καθορίζουν ένα συγκεκριμένο μοτίβο παρεμβολών δύο φωτονίων. Με άλλα λόγια, σε αυτόν τον τύπο κοινής και συσχετισμένης καταχώρησης θέσεων ανίχνευσης φωτονίων, εάν επιλεγεί διαφορετική θέση ανίχνευσης ενός φωτονίου, το μοτίβο παρεμβολών δύο φωτονίων παρουσιάζει μετατόπιση. Εάν καταγράφονται μόνο μεμονωμένα φωτόνια σε κάθε οθόνη χωρίς να υπάρχει συσχέτιση μεταξύ των θέσεων ανίχνευσής τους, τότε το μοτίβο παρεμβολών δεν σχηματίζεται σε κάθε οθόνηΠαρεμβολή δύο φωτονίων...Για να μάθετε μια παρέμβαση δύο φωτονίων στο πείραμα double-double-slit για ένα πεπερασμένο πλάτος κάθε σχισμής, λάβετε υπόψη ότι μια πηγή φωτονίων που βρίσκεται στην προέλευση παράγει μια κβαντική κατάσταση δύο φωτονίων ως φαίνεται στο Σχ. 1 . Οι διπλές σχισμές μπορούν να οριστούν από τις λειτουργίες μετάδοσης πλάτους και της διπλής σχισμής 1 και της διπλής σχισμής 2 αντίστοιχα. Όπου και είναι τα αυθαίρετα σημεία στη διπλή σχισμή 1 και τη διπλή σχισμή 2, αντίστοιχα έτσι ώστε η βάση θέσης να αντιστοιχεί σε αυτά τα σημεία που βρίσκονται στις διπλές σχισμές όπου ένα φωτόνιο μπορούν να βρεθούν είναι και | Ψ ⟩ t_ {1} (y ') t_ {2} (y ") y" y " | l_ {1}, y" \ rangle | l_ {2}, y "\ rangle A_ { 12} o_ {1} o_ {2} τ 1 ( ε ′ ) τ 2 ( ε ′ ′ ) ε ′ ε ′ ′ | μεγάλο 1 , ε ′ ⟩ | μεγάλο 2 , ε ′ ′ ⟩ . Επομένως, το εύρος για εύρεση φωτονίων στα σημεία και μαζί στις οθόνες μπορεί να γραφτεί ως ΕΝΑ 12 ο 1 ο 2 ΕΝΑ 12 = ∫ ∞ - ∞ ∫ ∞ - ∞ ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ τ 2 ( ε ′ ′ ) ⟨ μεγάλο 2 , ε ′ ′ | ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ τ 1 ( ε ′ ) ⟨ μεγάλο 1 , ε ′ | Ψ ⟩ ρε ε ′ ρε ε ′ ′ (2) Ας υποθέσουμε ότι η πηγή φωτονίων έχει πεπερασμένο μέγεθος και η κβαντική κατάσταση δύο φωτονίων είναι μια κβαντική κατάσταση εμπλεκόμενη στην ορμή, όπου και τα δύο φωτόνια έχουν την ίδια γραμμική πόλωση και συχνότητα. Μια τέτοια κβαντική κατάσταση εμπλοκής δύο φωτονίων μπορεί να παραχθεί από εκφυλισμένο μη γραμμικό SPDC με αντιστοίχιση φάσης τύπου Ι σε κρύσταλλο βήτα-βορικού βορικού (BBO) ο οποίος αντλείται από μια ακτίνα λέιζερ που διαδίδεται κατά μήκος του z- άξονα (διαμήκη κατεύθυνση), όπου το z- άξονας (δεν φαίνεται στο Σχ. 1 ) είναι κάθετο προς το xy | Ψ ⟩ -πλάνο (εγκάρσιο επίπεδο). Τα φωτόνια που είναι γνωστά ως το σήμα και τα αδρανή φωτόνια εκπέμπονται από την πηγή με αντίθετη ροπή με σχεδόν ίσο μέγεθος στο εγκάρσιο επίπεδο έτσι ώστε η κατάσταση εμπλοκής των δύο-φωτονίων στο χώρο της εγκάρσιας ορμής να είναι 42 , 43 , 44 , 45 , 46 | Ψ ⟩ = Ν ∫ ∫ ρε ε μικρό ρε ε Εγώ Φ ( ε μικρό , ε Εγώ ) | ε μικρό ⟩ | ε Εγώ ⟩ (3) όπου , είναι οι εγκάρσιες κβαντικές καταστάσεις ορμής του σήματος και τα αδρανή φωτόνια της ορμής και , αντίστοιχα και το Ν είναι μια σταθερά κανονικοποίησης. κύματος δύο φωτονίων αντιπροσωπεύει το εύρος για την εύρεση ενός φωτονίου σήματος σε κατάσταση ορμής και ένα αδρανές φωτόνιο σε κατάσταση ορμής . Η κβαντική εμπλοκή εκδηλώνεται από τη μη διαχωρισσιμότητα των | ε μικρό ⟩ | ε Εγώ ⟩ ε μικρό ε Εγώ \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}}}) | \ mathbf {q_ {s}} \ rangle | \ mathbf {q_ {i}} \ rangle \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}} }) \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}}}) Φ ( ε μικρό , ε Εγώ ) | ε μικρό ⟩ | ε Εγώ ⟩ Φ ( ε μικρό , ε Εγώ ) . Για την ακτίνα λέιζερ της αντλίας με προφίλ έντασης gaussian πεπερασμένου πλάτους στο εγκάρσιο επίπεδο, η δύο φωτονίων είναι εμφανής μόνο για καταστάσεις ορμής των φωτονίων με αντίθετη εγκάρσια ροπή. Δεδομένου ότι το μέγεθος της πηγής είναι πεπερασμένο, εάν η ορμή ενός φωτονίου μετριέται ακριβώς τότε η κβαντική κατάσταση του άλλου φωτονίου αντιστοιχεί σε μια κατάσταση ορμής αντίθετης ορμής με πεπερασμένη αβεβαιότητα. Περαιτέρω λεπτομέρειες σχετικά με την ορμή εμπλοκής των φωτονίων που παράγονται από εκφυλισμένο μη γραμμικό SPDC στον κρύσταλλο BBO δίδονται με μεθόδους. Φ ( ε μικρό , ε Εγώ ) Υπάρχουν δύο δυνατότητες που μπορούν να οδηγήσουν σε από κοινού ανίχνευση φωτονίων στην οθόνη 1 και στην οθόνη 2. Αυτές οι διακριτές δυνατότητες είναι (i) το φωτονίο σήματος διέρχεται μέσω διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1 και το αδρανές φωτόνιο διέρχεται μέσω διπλού - slit 2 και ανιχνεύεται στην οθόνη 2 και (ii) το αδρανές φωτόνιο διέρχεται μέσω της διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1 και το φωτονίο σήματος διέρχεται μέσω της διπλής σχισμής 2 και ανιχνεύεται στην οθόνη 2. Οποιοδήποτε μεμονωμένο φωτόνιο (σήμα ή idler) που μπορεί να ανιχνευθεί αφού περάσει από τη διπλή σχισμή 1 επισημαίνεται ως φωτόνιο 1 και οποιοδήποτε μεμονωμένο φωτόνιο που μπορεί να ανιχνευθεί μετά τη διέλευση από τη διπλή σχισμή 2 επισημαίνεται ως φωτόνιο 2. Το φωτόνιο 1 και το φωτόνιο 2 δεν μπορούν να διακριθούν καθώς έχουν την ίδια συχνότητα και πόλωση. Εξετάστε, η λειτουργία μετάδοσης της διπλής σχισμής 1 είναι τ 1 ( ε ′ ) = ένα ′ τ ( μι - ( ε ′ - ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 + μι - ( ε ′ + ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 ) , που αντιπροσωπεύει δύο γκάους σχισμές με διαχωρισμό μεταξύ τους και πλάτος σχισμής κάθε σχισμής είναι τέτοιο που είναι σημαντικά μεγαλύτερο από το . Παρομοίως, η λειτουργία μετάδοσης της διπλής σχισμής 2 είναι , ρε 1 σ 1 ρε 1 σ 1 τ 2 ( ε ′ ′ ) = ένα ′ ′ τ ( μι - ( ε ′ ′ - ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 + μι - ( ε ′ ′ + ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 ) ρε 2 σ 2 κάθε σχισμής είναι τέτοιο που είναι σημαντικά μεγαλύτερο από το . Όπου, και είναι οι σύνθετοι πολλαπλασιαστές των λειτουργιών μετάδοσης, περιλαμβάνουν τη μετατόπιση φάσης που εισάγεται από τις σχισμές και περιορίζει τη μέγιστη μετάδοση σε μία. Για , η μετάδοση των σχισμών είναι μηδέν. Κάθε διπλή σχισμή τοποθετείται πολύ μακριά από την πηγή σε σύγκριση με τον διαχωρισμό των σχισμών. Επομένως, οι σχισμές βρίσκονται σε στενή κλίση με το x ρε 2 σ 2 ένα ′ τ ένα ′ ′ τ ένα ′ τ = ένα ′ ′ τ = 0 - άξονας έτσι ώστε τα φωτόνια που προέρχονται από την πηγή να εμφανίζονται σε σχισμές σχεδόν κοντά στην κανονική συχνότητα. Για να έχει εμπλοκή διαδρομής δύο φωτονίων μέσω των σχισμών, οι διπλές σχισμές είναι τοποθετημένες έτσι ώστε και . Επιπλέον, η αβεβαιότητα της συνιστώσας ορμής κάθε φωτονίου παράλληλη με τις διπλές σχισμές, υπό την προϋπόθεση ότι η ορμή του άλλου φωτονίου προσδιορίζεται με ακρίβεια, είναι τόσο μικρή ώστε για την καταστολή της παρεμβολής ενός φωτονίου από κάθε διπλή σχισμή, όπου q είναι το μέγεθος της ορμής ενός φωτονίου 41 . Ωστόσο, ρε 1 / μεγάλο 1 = ρε 2 / μεγάλο 2 σ 1 / μεγάλο 1 = σ 2 / μεγάλο 2 Δ ε ∥ Δ ε ∥ / ε ≪ ρε 1 / μεγάλο 1 = ρε 2 / μεγάλο 2 Δ ε ∥ / ε ≈ σ 1 / μεγάλο 1 = σ 2 / μεγάλο 2 . Αυτές οι συνθήκες υπονοούν, εάν ένα φωτόνιο διέρχεται μέσω σχισμής τότε το άλλο φωτονίο περνά πιθανότατα μέσω σχισμής και εάν ένα φωτόνιο διέρχεται μέσω σχισμής το άλλο φωτόνιο πιθανότατα περνάει από τη σχισμή . Επομένως, τα φωτόνια που συμβάλλουν στην ανίχνευση αρθρώσεων στις οθόνες εμπλέκονται μέσω των σχισμών. Ωστόσο, εάν ένα φωτόνιο απορροφάται πολύ μακριά από σχισμές σε αυθαίρετη θέση στη διπλή σχισμή 1, τότε το άλλο φωτόνιο πιθανότατα απορροφάται στο ένα 1 σι 2 σι 1 ένα 2 ε ′ ε ′ ′ = - ε ′ μεγάλο 2 / μεγάλο 1 πολύ μακριά από σχισμές διπλής σχισμής 2. Η μετάδοση κάθε σχισμής θεωρείται γκάους με πολύ μικρό πλάτος που επιτρέπει σε ένα φωτόνιο να περάσει μέσα από αυτό. Υπό αυτές τις εκτιμήσεις, το εύρος της κοινής ανίχνευσης των φωτονίων στις οθόνες λαμβάνει σημαντική συνεισφορά από ένα μικρό εύρος καταστάσεων ορμής της κβαντικής κατάστασης . Οι υπόλοιπες καταστάσεις ορμής στο απορροφώνται σε διπλές σχισμές. Επομένως, για να αξιολογήσετε χρησιμοποιώντας το Εξ. 2 , μπορεί να εφαρμοστεί μια ακόλουθη προσέγγιση ΕΝΑ 12 | Ψ ⟩ | Ψ ⟩ ΕΝΑ 12 τ 2 ( ε ′ ′ ) τ 1 ( ε ′ ) ⟨ μεγάλο 2 , ε ′ ′ | ⟨ μεγάλο 1 , ε ′ | Ψ ⟩ ≈ ένα ′ ′ τ ένα ′ τ ντο β ( μι Εγώ ε ( ρ ένα 1 + ρ σι 2 ) / ℏ ⋅ μι - ( ε ′ - ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 μι - ( ε ′ ′ + ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 + μι Εγώ ε ( ρ σι 1 + ρ ένα 2 ) / ℏ ⋅ μι - ( ε ′ + ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 μι - ( ε ′ ′ - ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 ) (4) όπου είναι μια σταθερά αναλογικότητας που εξαρτάται από τη λειτουργία κύματος δύο φωτονίων. Δεδομένου ότι τα φωτόνια εμφανίζονται σε κάθε σχισμή κοντά στην κανονική συχνότητα εμφάνισης, το είναι το πλάτος δύο φωτονίων ενός φωτονίου για μετάβαση από την πηγή για σχισμή βρίσκεται σε απόσταση και άλλο φωτονίο για μετάβαση από την πηγή στη σχισμή βρίσκεται σε απόσταση . Παρομοίως, το είναι το πλάτος δύο φωτονίων ενός φωτονίου για μετάβαση από την πηγή στην σχισμή βρίσκεται στο μια απόσταση και άλλα φωτόνια για μετάβαση από την πηγή στη σχισμή ντο β μι Εγώ ε ( ρ ένα 1 + ρ σι 2 ) / ℏ ένα 1 ρ ένα 1 σι 2 ρ σι 2 μι Εγώ ε ( ρ σι 1 + ρ ένα 2 ) / ℏ σι 1 ρ σι 1 ένα 2 r_ {a2} a_ {1} a_ {2} b_ {1} b_ {2} \ Phi (\ mathbf {q_ {s} , \ mathbf {q_ {i}}}) βρίσκεται σε απόσταση . Το μεταδιδόμενο πλάτος των φωτονίων μέσω των σχισμών και ή μέσω των σχισμών και είναι αμελητέο επειδή είναι πολύ μικρό για αυτές τις διαδρομές. Τα φωτόνια εμπλέκονται μέσω των σχισμών και της εξίσωσης. 4 αντιπροσωπεύει το πλάτος των μεταδιδόμενων φωτονίων στις διπλές σχισμές που οδηγούν στην κοινή ανίχνευση των φωτονίων. ρ ένα 2 ένα 1 ένα 2 σι 1 σι 2 Φ ( ε μικρό , ε Εγώ ) Το μεταδιδόμενο πλάτος φωτονίου ενός φωτονίου προέρχεται περαιτέρω από ένα σημείο σε μια διπλή σχισμή έτσι ώστε να αντιστοιχεί σε μια ομοιόμορφη κατανομή πιθανότητας του φωτονίου που βρίσκεται στην οθόνη. Τα πλάτη των μεταδιδόμενων φωτονίων για μετάβαση από μια θέση σημείου σε μια διπλή σχισμή σε μια θέση σημείου στην πλησιέστερη οθόνη είναι και για το φωτόνιο 1 και το φωτόνιο 2, αντίστοιχα. Όπου και είναι οι αποστάσεις και από αυθαίρετα σημεία και ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ ∝ μι Εγώ ε | Ρ ′ | / ℏ / | Ρ ′ | 1 / 2 ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ ∝ μι Εγώ ε | Ρ ′ ′ | / ℏ / | Ρ ′ ′ | 1 / 2 Ρ ′ Ρ ′ ′ ο 1 ο 2 ε ′ ε ′ ′ βρίσκεται σε διπλή σχισμή 1 και διπλή σχισμή 2, αντίστοιχα. Δεδομένου ότι οι αποστάσεις και των οθονών από τις πλησιέστερες διπλές σχισμές είναι πολύ μεγαλύτερες από τις διαχωριστικές σχισμές, επομένως, και , όπου και είναι οι αποστάσεις και από τα μεσαία σημεία της διπλής σχισμής 1 και της διπλής σχισμής 2, αντίστοιχα όπως φαίνεται στο Σχ. 1 . Μετά την επίλυση Εξ. 2 μικρό 1 μικρό 2 ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ ∝ μι Εγώ ε ( ρ 1 - ε ′ αμαρτία ( θ 1 ) ) / ℏ / ρ 1 / 2 1 ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ ∝ μι Εγώ ε ( ρ 2 - ε ′ ′ αμαρτία ( θ 2 ) ) / ℏ / ρ 1 / 2 2 ρ 1 ρ 2 ο 1 ο 2 χρησιμοποιώντας το Εξ. 4 το εύρος της κοινής ανίχνευσης των φωτονίων μπορεί να γραφτεί ως ΕΝΑ 12 = ντο ν μι Εγώ ε ( ρ 1 + ρ 2 ) / ℏ μι Εγώ ε ( ρ ένα 1 + ρ σι 2 + ρ ένα 2 + ρ σι 1 ) / 2 ℏ ( ρ 1 ρ 2 ) 1 / 2 μι - ε 2 ( ( σ 1 αμαρτία θ 1 ) 2 + ( σ 2 αμαρτία θ 2 ) 2 ) / 2 ℏ 2 συν [ ε ( ρε 2 αμαρτία θ 2 - ρε 1 αμαρτία θ 1 ) / 2 ℏ + δ ] (5) όπου και είναι σταθερά αναλογικότητας. Επομένως, η πιθανότητα ανίχνευσης σύμπτωσης των φωτονίων είναι δ = ε ( ρ ένα 1 + ρ σι 2 - ρ ένα 2 - ρ σι 1 ) / 2 ℏ ντο ν Π 12 = | ΕΝΑ 12 | 2 Π 12 = | ντο ν | 2 ρ 1 ρ 2 μι - ε 2 ( ( σ 1 αμαρτία θ 1 ) 2 + ( σ 2 αμαρτία θ 2 ) 2 ) / ℏ 2 συν 2 [ ε ( ρε 2 αμαρτία θ 2 - ρε 1 αμαρτία θ 1 ) / 2 ℏ + δ ] (6) Η πιθανότητα της σύμπτωσης ανίχνευσης των φωτονίων είναι ένα προϊόν δύο συναρτήσεων, όπου οι εκθετικές συναρτήσεις αντιστοιχούν σε μια περίθλαση ενός φωτονίου ενός φωτονίου από μονές σχισμές και μια λειτουργία συνημίτου αντιστοιχεί σε παρεμβολές δύο φωτονίων από τη διπλή σχισμή. Δεδομένου ότι τα φωτόνια εμπλέκονται στις διαδρομές μέσω των σχισμών, επομένως, Εξ. 6δεν μπορεί να γραφτεί ως προϊόν δύο ξεχωριστών συναρτήσεων μεταβλητών του φωτονίου 1 και του φωτονίου 2, αντίστοιχα. Εάν καταγράφονται μόνο οι μεμονωμένες θέσεις ανίχνευσης φωτονίων σε κάθε οθόνη χωρίς να υπάρχει συσχετισμός μεταξύ τους, τότε δεν σχηματίζεται μοτίβο παρεμβολών. Μια μεμονωμένη παρεμβολή φωτονίου καταστέλλεται λόγω της κβαντικής εμπλοκής των διαδρομών των φωτονίων στη διπλή σχισμή. Και τα δύο φωτόνια μπορούν να ανιχνευθούν οπουδήποτε τυχαία στις αντίστοιχες οθόνες, ωστόσο, ένα κβαντικό σχέδιο παρεμβολών δύο φωτονίων εμφανίζεται μόνο στις μετρήσεις που σχετίζονται με τη θέση. Η πιθανότητα ανίχνευσης ενός μεμονωμένου φωτονίου στις αντίστοιχες οθόνες μπορεί να υπολογιστεί ενσωματώνοντας όλες τις πιθανές διαδρομές ενός μεμονωμένου φωτονίου. Ωστόσο, Λόγω της κβαντικής εμπλοκής των διαδρομών, αυτό το ακέραιο αποτέλεσμα οδηγεί σε προσθήκη πιθανότητας ανίχνευσης ενός μόνο φωτονίου μέσω κάθε σχισμής διπλής σχισμής. Επομένως, οι πιθανότητες Π 1 και για να βρείτε ένα μόνο φωτόνιο στην οθόνη 1 και στην οθόνη 2 είναι Π 2 Π 1 ∝ 1 ρ 1 μι - ε 2 ( σ 1 αμαρτία θ 1 ) 2 / ℏ 2 (7α) Π 2 ∝ 1 ρ 2 μι - ε 2 ( σ 2 αμαρτία θ 2 ) 2 / ℏ 2 (7β) όπου κάθε κατανομή πιθανότητας μιας ανίχνευσης ενός φωτονίου είναι gaussian και δεν εμφανίζεται ένα μοτίβο παρεμβολής με ένα φωτονίο. Το πραγματικό πείραμα εκτελείται στον τρισδιάστατο χώρο θέσης, όπου η ορμή των φωτονίων και οι αποστάσεις των ανιχνευτών από διπλές σχισμές μετρούνται στον τρισδιάστατο χώρο θέσης. Επομένως, η προβολή της ορμής και των αποστάσεων στο εγκάρσιο επίπεδο θα πρέπει να λαμβάνεται υπόψη ώστε να είναι συνεπής με τις εξισώσεις. 6 και 7 . Στο πραγματικό πείραμα οι σχισμές βρίσκονται παράλληλα με το εγκάρσιο επίπεδο, η μετατόπιση του ανιχνευτή είναι παράλληλη με το εγκάρσιο επίπεδο και το εύρος μετατόπισης είναι τέτοιο ώστε , επομένως, και ε 1 ≪ μικρό 1 ε 2 ≪ μικρό 2 αμαρτία θ 1 ∼ ε 1 / μικρό 1 αμαρτία θ 2 ∼ ε 2 / μικρό 2 . Υπό αυτές τις εκτιμήσεις, οι όροι με τη μορφή αναλογίας, εγκάρσιας ορμής και απόστασης οθόνης από αντίστοιχη διπλή σχισμή, εμφανίζονται στα Εξ. 6 και 7 . Επομένως, η ορμή των φωτονίων και οι αποστάσεις των ανιχνευτών από διπλές σχισμές που μετρώνται στον τρισδιάστατο χώρο θέσης μπορούν να τοποθετηθούν σε αυτές τις εξισώσεις για τον υπολογισμό των σχεδίων. Πείραμα Το πείραμα διπλής σχισμής που παρουσιάζεται σε αυτό το έγγραφο εκτελείται με φωτονικά εμπλεγμένα με ορμή που παράγονται από εκφυλισμένο μη-γραμμικό SPDC 21 , 24 , 39 , 42 , 43 , 44 , 45 , 47 . Ο κρύσταλλος BBO αντλείται από μια εξαιρετική γραμμικά πολωμένη ακτίνα λέιζερ μήκους κύματος 405 nm και κάτω ζεύγη φωτονίων μήκους κύματος 810 nm με συνηθισμένη πόλωση παράγονται κατά την εμπρόσθια κατεύθυνση σε σχήμα κωνικής εκπομπής σύμφωνα με την ορμή και την εξοικονόμηση ενέργειας όπως φαίνεται στο Σχ. 2. Για να δημιουργήσετε μια εικονική διαμόρφωση διπλής σχισμής, δύο διπρισμοί Fresnel τοποθετούνται στη διαδρομή των φωτονίων και τα φωτόνια ανιχνεύονται από φωτοανιχνευτές χιονοστιβάδας με ένα φωτονίο και ρε 1 ρε 2 . Τα οπτικά φίλτρα στενής ζώνης τοποθετούνται μπροστά από κάθε ανιχνευτή φωτονίων για να σταματήσει το φως του φόντου. Τα φωτόνια που έχουν μετατραπεί κάτω έχουν την ίδια συχνότητα και γραμμική πόλωση, η οποία είναι κάθετη με την πόλωση της δέσμης λέιζερ της αντλίας. Η ένταση του λέιζερ της αντλίας είναι τέτοια που η πιθανότητα παραγωγής περισσότερων από ένα ζεύγος φωτονίων είναι εξαιρετικά μικρή. Ο αριθμός των μετρήσεων φωτονίων κάθε ανιχνευτή φωτονίων και οι μετρήσεις αμοιβαίας σύμπτωσής τους μετρώνται με μια μονάδα μέτρησης δύο καναλιών μονής φωτονίας. Η επέκταση εγκάρσιου τρόπου λειτουργίας της δέσμης λέιζερ της αντλίας μειώνεται για να διατηρηθεί το μέγεθος της πηγής πολύ μικρότερο από το διαχωρισμό των σχισμών, αλλά είναι μεγάλο έτσι ώστε να διατηρείται η ορμή εμπλοκής των φωτονίωνΣχήμα
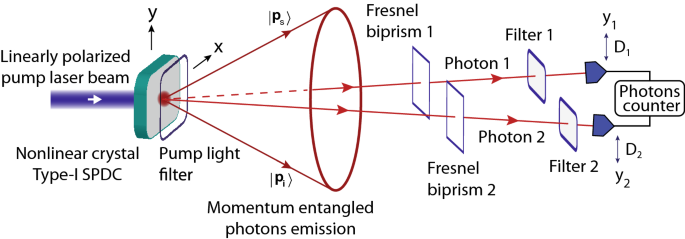
Ένα σχηματικό διάγραμμα της πειραματικής διαμόρφωσης του πειράματος double-double-slit. Τα ζεύγη φωτονίων που εμπλέκονται σε ορμή παράγονται σε κωνικό μοτίβο εκπομπών από μη γραμμικό κρύσταλλο. Μια διαμόρφωση διπλής σχισμής πραγματοποιείται με δύο διμερισμούς FresnelΣχήμα
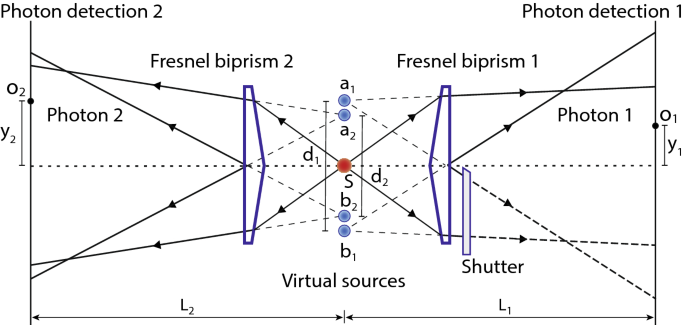
Ένα ξεδιπλωμένο διάγραμμα του πειράματος double-double-slit που πραγματοποιήθηκε με διπρισμούς Fresnel. Οι εικονικές πηγές αντιστοιχούν σε εικονικές σχισμές. Για να ανιχνεύσει ποια διαδρομή διαδρομής των φωτονίων, ένα κλείστρο μπορεί να τοποθετηθεί σε μια διαδρομή του φωτονίου 1 με τέτοιο τρόπο ώστε να αποκλείεται μια εικονική σχισμή . σι 1
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Wednesday, July 08, 2020
Μελέτη βελτίωσης των παραμέτρων απόδοσης μιας νέας κεραίας 0,41-0,47 THz on-chip με βάση την έννοια της επιφάνειας των μετρήσεων που υλοποιήθηκε σε στρώμα GaAs 50 μm
Παρουσιάζεται μια μελέτη σκοπιμότητας σχετικά με τις παραμέτρους απόδοσης μιας νέας κεραίας on-chip που βασίζεται στην τεχνολογία metasurface στη ζώνη terahertz. Η προτεινόμενη κεραία on-chip metasurface είναι κατασκευασμένη σε ένα ηλεκτρικά λεπτό στρώμα υποστρώματος αρσενιδίου γαλλίου υψηλής διαπερατότητας (GaAs). Το Metasurface υλοποιείται με χαρακτική γραμμές υποδοχής σε μια σειρά κυκλικών μπαλωμάτων 11 × 11 κατασκευασμένα στο πάνω στρώμα του υποστρώματος GaAs και μεταλλικές οπές που εφαρμόζονται στο κεντρικό έμπλαστρο κάθε σειράς που αποτελεί τη συστοιχία, η οποία συνδέει το έμπλαστρο με τη διαρροή - κυματοειδείς γραμμές τροφοδοσίας ανοιχτού τύπου που τρέχουν κάτω από τα μπαλώματα. Οι γραμμές αυλακώσεων συνδέονται μεταξύ τους με σχισμή. Μια θύρα κυματοδηγού χρησιμοποιείται για να διεγείρει τη συστοιχία μέσω γραμμών υποδοχής που συνδέουν την ηλεκτρομαγνητική ενέργεια με τα μπαλώματα. Η κεραία on-chip metasurface φαίνεται να εμφανίζει ένα μέσο μετρούμενο κέρδος άνω των 10 dBi και απόδοση ακτινοβολίας πάνω από 60% σε ένα ευρύ φάσμα συχνοτήτων από 0,41 έως 0,47 THz, κάτι που είναι σημαντική ανάπτυξη σε σχέση με άλλες τεχνικές κεραίας on-chip που έχουν αναφερθεί μέχρι σήμερα . Οι διαστάσεις της κεραίας είναι 8,6 × 8,6 × 0,0503 mm3 . Τα αποτελέσματα δείχνουν ότι η προτεινόμενη κεραία metasurface με βάση GaAs είναι βιώσιμη για εφαρμογές σε ολοκληρωμένα κυκλώματα terahertz.
Εισαγωγή
Η ζώνη συχνοτήτων terahertz (THz) που εκτείνεται στις συχνότητες μεταξύ 0,1 και 10 THz προσφέρει πιθανές εφαρμογές σε διάφορους κλάδους, όπως ιατρική επιστήμη 1 , απεικόνιση 2 , άμυνα και ασφάλεια 3 , φασματοσκοπία χρονικού τομέα 4 , αστρονομία 5 , γεωργία 6 και ασύρματη επικοινωνία συστήματα 7 . Κεραίες βασισμένες στο Planar Fabry – Perot cavity έχουν αποδειχθεί στη ζώνη THz και τέτοιες κεραίες έχουν χαρακτηριστικό ακτινοβολίας υψηλής κατευθυντικότητας 8 , 9. Δυστυχώς, ο σχεδιασμός και η κατασκευή αυτών των κεραιών μπορεί να είναι περίπλοκος και η απόδοση ακτινοβολίας τους είναι σχετικά χαμηλή ειδικά όταν εφαρμόζεται σε υποστρώματα υψηλής διαπερατότητας 10 . Παρ 'όλα αυτά, οι συγγραφείς στα 11 έχουν επιδείξει με επιτυχία μια κεραία Fabry – Perot κοιλότητας στη ζώνη THz που είναι σχετικά πιο εύκολο να κατασκευαστεί και εμφανίζει υψηλή απόδοση κατεύθυνσης και απόδοσης. Στη ζώνη συχνοτήτων terahertz ένα ηλεκτρικά παχύ υπόστρωμα δημιουργεί ανεπιθύμητο συντονισμό στο υπόστρωμα. Έχει δειχθεί ότι αυτές οι συντονισμοί μπορούν να αποφευχθούν με την απλή μείωση του πάχους του υποστρώματος από λ 0 /20, όπου το λ 0 αντιπροσωπεύει το μήκος κύματος του ελεύθερου χώρου 12 .
Το Metasurface μπορεί ουσιαστικά να δημιουργηθεί με τη διανομή ηλεκτρικά μικρών αντικειμένων σκέδασης πάνω στην επιφάνεια ενός διηλεκτρικού μέσου που ουσιαστικά διαταράσσει τη διάδοση ηλεκτρομαγνητικών κυμάτων 13 . Στην πραγματικότητα, το γεωμετρικό σχήμα των αντικειμένων σκέδασης καθορίζει τις ηλεκτρομαγνητικές ιδιότητες του μετα-υλικού 14 . Οι κεραίες που εφαρμόστηκαν χρησιμοποιώντας δομές μετα-υλικών ή μετα-επιφάνειας έχουν αποδειχθεί ότι βελτιώνουν την απόδοση της κεραίας όσον αφορά το κέρδος ακτινοβολίας, την απόδοση ακτινοβολίας, το μοτίβο ακτινοβολίας και το εύρος ζώνης 15 . Τα αποτελέσματα αυτών των ερευνών αποκαλύπτουν ότι αυτή η τεχνολογία μπορεί να εφαρμοστεί για την πραγματοποίηση κεραιών terahertz καθιστώντας τις βιώσιμες για πρακτικές εφαρμογές.
Τα σήματα THz αντιμετωπίζουν πολύ μεγαλύτερη εξασθένηση και ατμοσφαιρική απώλεια σε σύγκριση με τους συμβατικούς συνδέσμους μικροκυμάτων. Ως εκ τούτου, οι δομές κεραιών με υψηλό κέρδος και προδιαγραφές υψηλής απόδοσης είναι απαραίτητες στην περιοχή THz. Αυτό το άρθρο παρουσιάζει μια μελέτη σκοπιμότητας μιας κεραίας THz on-chip που βασίζεται στο metasurface concept για τη βελτίωση του εύρους ζώνης, της απόδοσης ακτινοβολίας και των χαρακτηριστικών απόδοσης. Η προτεινόμενη κεραία on-chip metasurface λειτουργεί σε πολύ υψηλότερη συχνότητα (410-470 GHz), την οποία γνωρίζουν οι συγγραφείς για πρώτη φορά.
Διαδικασία σχεδιασμού της κεραίας μετα-επιφάνειας on-chip
Η διαμόρφωση της κεραίας αναφοράς σε τσιπ που περιλαμβάνει μια σειρά κυκλικών μπαλωμάτων 11 × 11 χωρίς τις υποδοχές μετα-επιφάνειας φαίνεται στο Σχ. 1 α. Τα στοιχεία ακτινοβολίας της κεραίας αναφοράς σε τσιπ αποτελούνται από κυκλικά επιθέματα που εφαρμόζονται σε ένα ηλεκτρικά λεπτό στρώμα αρσενιδίου γαλλίου υψηλής διαπερατότητας (GaAs). Ομοίως, η διαμόρφωση της προτεινόμενης κεραίας on-chip στο Σχ. 1Το b αποτελείται από μια σειρά κυκλικών μπαλωμάτων 11 × 11, ωστόσο αυτά τα μπαλώματα είναι ενσωματωμένα με γραμμές υποδοχής διαφόρων μηκών για να δημιουργήσουν μια δομή μετα-επιφάνειας. Και στις δύο περιπτώσεις οι κεραίες κατασκευάζονται συγκεντρώνοντας στρώματα μεταλλοποίησης-GaAs-επιμετάλλωσης. Κάθε κεντρικό επίθεμα ακτινοβολίας τρυπιέται με μια μεταλλική οπή μέσω στο κέντρο του δημιουργώντας έτσι μια διαδρομή RF που συνδέει το έμπλαστρο με την ανοιχτή γραμμή υποδοχής στο επίπεδο του εδάφους μέσω του στρώματος υποστρώματος GaAs. Κατά συνέπεια, η δομή της κεραίας διεγείρεται μέσω των ανοικτών στενών γραμμών εγκοπών που είναι διαμορφωμένες στην κάτω πλευρά του στρώματος υποστρώματος GaAs, οι οποίες ευθυγραμμίζονται ακριβώς κάτω από κάθε σειρά των συστοιχιών επιθέματος ακτινοβολίας που αποτελούν την κεραία, όπως φαίνεται στο Σχ. . 1CD. Στον προτεινόμενο μηχανισμό τροφοδοσίας, η κεντρική μεταλλική οπή μέσω σύνδεσης συνδέεται με μια θύρα συμπαγούς κυματοδηγού (CPW) και στη συνέχεια όλες οι μεταλλικές οπές μέσω σύνδεσης συνδέονται ηλεκτρομαγνητικά μεταξύ τους μέσω της σχισμής του επιπέδου εδάφους όπως φαίνεται στο Σχ. 1ντο. Όταν η θύρα CPW είναι ενθουσιασμένη, προκαλεί τη ροή της ηλεκτρομαγνητικής ενέργειας πάνω από τις ανοιχτές γραμμές υποδοχής με κύματα διαρροής και αυτή η ενέργεια συνδέεται με τις κυκλικές συστοιχίες μπαλωμάτων μέσω των μεταλλικών διαμπερών οπών, προκαλώντας την εκπομπή ακτινοβολίας από την κεραία της επιφάνειας. Στο τμήμα III θα είναι προφανές ότι η δομή της επιφάνειας 2D αυξάνει ουσιαστικά την αποτελεσματική περιοχή ανοίγματος της κεραίας που ενισχύει τα χαρακτηριστικά ακτινοβολίας της χωρίς να αυξάνει τις φυσικές διαστάσεις της κεραίας. Επίσης, τα κύματα επιφανείας και οι απώλειες υποστρώματος καταστέλλονται σημαντικά χρησιμοποιώντας τον προτεινόμενο ηλεκτρομαγνητικό μηχανισμό τροφοδοσίας ζεύξης για να διεγείρουν τα επιθέματα ακτινοβολίας, με αποτέλεσμα τη βελτίωση της απόδοσης της κεραίας όσον αφορά το κέρδος ακτινοβολίας και την αποδοτικότητα στη ζώνη συχνότητας λειτουργίας.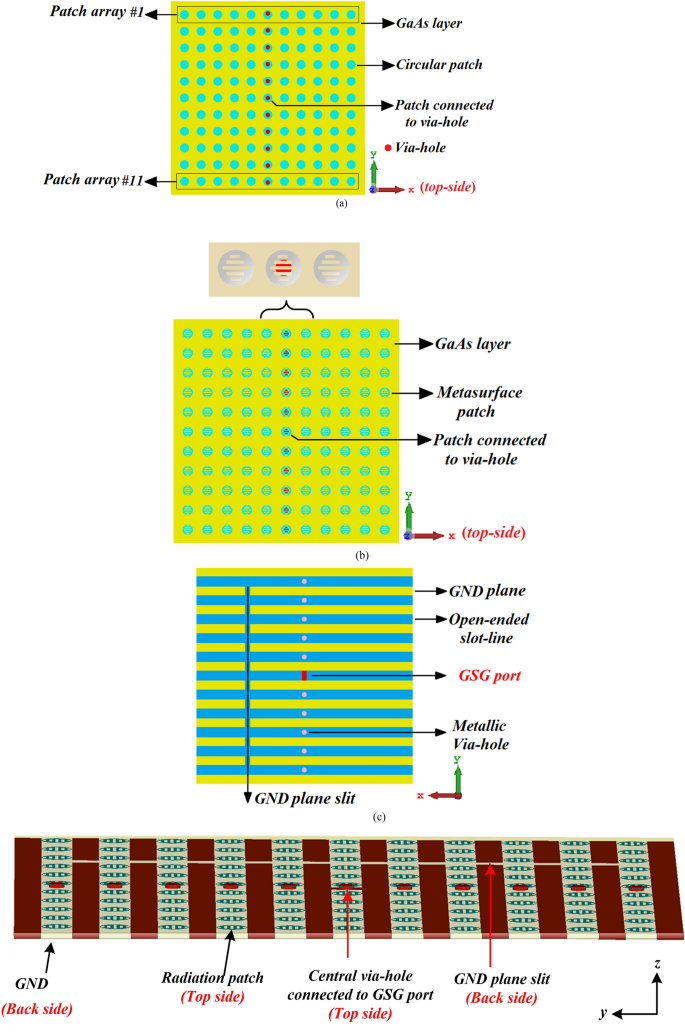 Σχ.
Σχ. 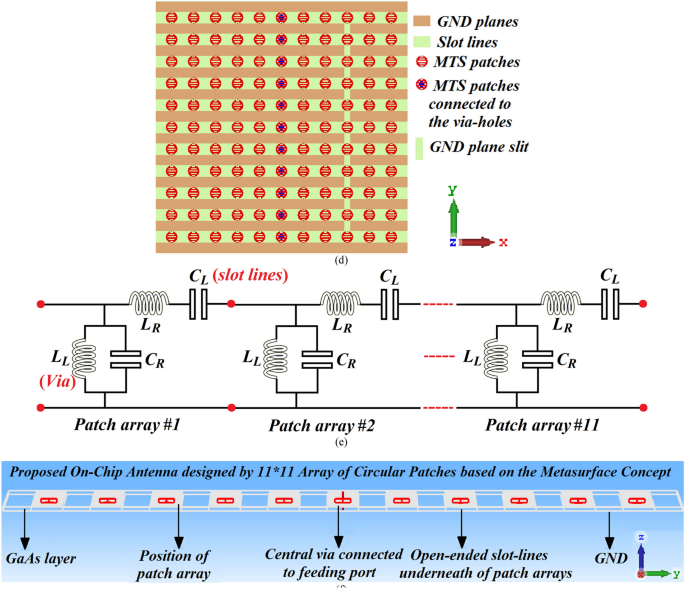
 Σχ.
Σχ. 
( α ) Διάταξη της κεραίας αναφοράς σε τσιπ που περιέχει μια σειρά κυκλικών μπαλωμάτων 11 × 11 χωρίς επιφανειακή επιφάνεια, κάτοψη, ( β ) διάταξη της προτεινόμενης κεραίας on-chip σχεδιασμένη από μια σειρά κυκλικών μπαλωμάτων 11 × 11 με επιφάνεια , κάτοψη, ( γ ) πίσω πλευρά των δύο δομών κεραίας αναφοράς και προτεινόμενης κεραίας. Η θύρα GSG συνδέεται στην κεντρική οπή και όλες οι μεταλλικές οπές συνδέονται ηλεκτρομαγνητικά μεταξύ τους μέσω της σχισμής του επιπέδου GND. ( δ ) 3D ισομετρική άποψη της προτεινόμενης δομής κεραίας on-chip με βάση την έννοια της επιφάνειας μετα-επιφάνειας, (το MTS αντιπροσωπεύει την επιφάνεια επιφάνειας), ( ε ) ισοδύναμο μοντέλο κυκλώματος της προτεινόμενης κεραίας on-chip και ( f) σχηματική άποψη της προτεινόμενης δομής.>>Το χρησιμοποιούμενο υπόστρωμα GaAs έχει διηλεκτρική σταθερά = 12.9, απώλεια εφαπτομένου του μαύρου = 0,006 και πάχος h = 50 (~ λ 0 /13, όπου το λ 0 είναι το μήκος κύματος του ελεύθερου χώρου με κέντρο το 0,44 THz). Τα αγώγιμα στοιχεία στις δομές κεραίας on-chip είναι αλουμίνιο με πάχος 0,35 και αγωγιμότητα 3,56 × 10 7 S / m. Τόσο η κεραία αναφοράς on-chip όσο και οι προτεινόμενες δομές κεραίας on-chip έχουν πανομοιότυπες διαστάσεις 8,6 × 8,6 × 0,0503 mm 3 . ε ρ δ \ mu \ text {m} \ mu \ text {m} μ Μ μ Μ Στην προτεινόμενη δομή μετα-επιφάνειας 2D, οι γραμμές υποδοχής συμπεριφέρονται ουσιαστικά ως αριστερή χωρητικότητα σειράς που προκύπτει από το στρώμα υποδοχής 16 . Το προτεινόμενο metasurface περιλαμβάνει μια μεταλλική οπή μέσω του κεντρικού επιθέματος κάθε σειράς επιθεμάτων που συνδέει το άνω στρώμα (μπαλώματα ακτινοβολίας) με το κάτω στρώμα (επίπεδο εδάφους) μέσω του στρώματος υποστρώματος GaAs. Αυτό εισάγει μια παρατεταμένη αριστερή αυτεπαγωγή. Η δομή εισάγει επίσης ανεπιθύμητα παρασιτικά αποτελέσματα που έχουν ως αποτέλεσμα τη διακλάδωση της δεξιόχειρης χωρητικότητας και της σειράς δεξιόχειρης επαγωγής 17 . Η διακλάδωση του δεξιού χεριού οφείλεται στην χωρητικότητα του κενού που δημιουργείται μεταξύ των επιπέδων ακτινοβολίας και του επιπέδου γείωσης, και η σειρά δεξιότητας επαγωγής δημιουργείται από τα αναπόφευκτα επιφανειακά ρεύματα 18. Το ισοδύναμο μοντέλο κυκλώματος της προτεινόμενης κεραίας on-chip που εφαρμόζει την αρχή της επιφάνειας των μετρήσεων παρουσιάζεται στο Σχ. 1 ε. Επιπρόσθετα, η σχηματική του άποψη παρουσιάζεται στο Σχ. 1 f για την καλύτερη αναγνώριση των κατασκευαστικών στοιχείων του. Η δομή της κεραίας διαμορφώθηκε σε έναν εμπορικά διαθέσιμο 3D EM full-wave solver (CST Microwave Studio ™) χρησιμοποιώντας τεχνική πεπερασμένης ολοκλήρωσης στον τομέα του χρόνου. Η δομή της κεραίας βελτιστοποιήθηκε για μεγάλο εύρος ζώνης σύνθετης αντίστασης, αύξηση ακτινοβολίας και απόδοση. Για την καλύτερη κατανόηση των επιδράσεων της επιφάνειας στην απόδοση της κεραίας on-chip , αναλύθηκε και συγκρίθηκε για πρώτη φορά μια κεραία αναφοράς με chip επιφάνεια χωρίς μεταεπιφάνεια που αποτελείται μόνο από τα κυκλικά επιθέματα χωρίς γραμμές, όπως φαίνεται στο σχήμα 1 a. κεραία on-chip με δομή μετα-επιφάνειας. Στην ενότητα III, φαίνεται ότι με τη μέτρηση της επιφάνειας υπάρχει μέση βελτίωση 10,8% και 39,2% στην απόδοση και στην απόδοση της ακτινοβολίας, αντίστοιχα. Οι αναλύσεις προσομοίωσης που πραγματοποιήθηκαν αποκάλυψαν ότι το κενό μεταξύ των εξόχως κυκλικών μπαλωμάτων και της άκρης του υποστρώματος είναι σημαντικό. Το διάκενο πρέπει να είναι περίπου ίσο με το διάστημα μεταξύ δύο γειτονικών μπαλωμάτων για την αποφυγή καταστροφικών παρεμβολών στο πλευρικό επίπεδο που προκύπτει από διαθλασμένα κύματα από την άκρη του υποστρώματος. Το κέρδος κεραίας ως συνάρτηση της συχνότητας διερευνήθηκε για τα διάφορα μεγέθη μήτρας κεραίας. Όπως αναμενόταν, το κέρδος της κεραίας είναι συνάρτηση του μεγέθους μήτρας των ακτινοβολούμενων στοιχείων, ωστόσο το οροπέδιο κέρδους με αυξανόμενο μέγεθος μήτρας. Αυτό μπορεί να εξηγηθεί με ερμηνεία διαρροής-κύματος αυτής της δομής, δηλαδή μόλις βρεθεί ο πολλαπλασιασμός διαρροής (σύνθετος) αριθμός κύματος. Η σταθερά εξασθένησης της λειτουργίας διαρροής θα καθορίσει το ελάχιστο μέγεθος κεραίας L για να ακτινοβολεί μια δεδομένη απόδοση ακτινοβολίας, δηλαδή 19 . η = 1 - μι - α μεγάλο Οι διαστάσεις της βελτιστοποιημένης κεραίας on-chip που κατασκευάζεται από μια σειρά κυκλικών μπαλωμάτων 11 × 11 είναι έτσι: το διάκενο μεταξύ των μπαλωμάτων είναι 200 μm, η ακτίνα του μπαλώματος είναι 200 μm, η ακτίνα μέσω οπών είναι 100 μm, το πλάτος της υποδοχής είναι 40 μm, το μήκος και Το πλάτος των ανοιχτών γραμμών είναι 8,6 mm και 0,4 mm, αντίστοιχα. Απόδοση κεραίας on-chip Metasurface Τα κατασκευασμένα πρωτότυπα της αναφοράς και οι προτεινόμενες κεραίες on-chip που εφαρμόστηκαν μέσω μιας σειράς κυκλικών μπαλωμάτων 11 × 11 και η απόδοση εύρους ζώνης αντίστασης τους φαίνονται στο Σχ. 2 . Τα χαρακτηριστικά της κεραίας μετρήθηκαν χρησιμοποιώντας ένα συμπαγές εύρος δοκιμής κεραίας όπως περιγράφεται στο 25 . Από τις καμπύλες συντελεστή ανάκλασης είναι προφανές ότι μετά την εφαρμογή της επιφάνειας μέτρησης το εύρος ζώνης αντίστασης της κεραίας και η απόδοση αντιστοίχισης σύνθετης αντίστασης βελτιώνονται σημαντικά. Η προτεινόμενη κεραία on-chip με γραμμές επιφάνειας μέτρησης έχει εύρος ζώνης αντίστασης από 0,41 έως 0,47 THz για S 11
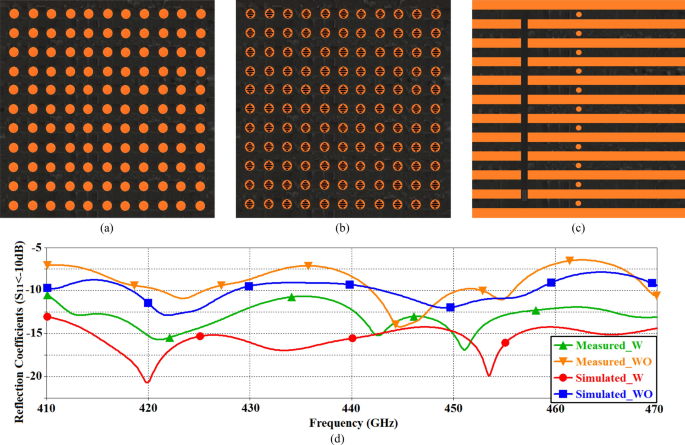
Κατασκευασμένα πρωτότυπα της αναφοράς, δηλαδή χωρίς (WO) υποδοχές μετα-επιφάνειας και τα προτεινόμενα, δηλαδή με (W) υποδοχές μετα-επιφάνειας, κεραίες on-chip. ( α ) Κάτοψη της κεραίας αναφοράς on-chip, ( β ) κάτοψη της προτεινόμενης κεραίας on-chip, ( γ ) οπίσθια όψη και των δύο κεραιών op-chip, και ( δ ) της προσομοίωσης και της μετρημένης αντανάκλασης - συντελεστής απόκρισηςΤα χαρακτηριστικά ακτινοβολίας της κεραίας on-chip μετρήθηκαν χρησιμοποιώντας ένα μικρό εύρος δοκιμών κεραίας όπως εξηγείται στο 20 . Οι τυποποιημένες διαδικασίες δοκιμής IEEE για κεραίες 21χρησιμοποιήθηκε για να κατασκευαστεί ένα ακριβές σύστημα μέτρησης κεραίας μακρινών πεδίων σε περιβάλλον σταθμού ανιχνευτή. Το πρωτότυπο της κεραίας τοποθετήθηκε σε σταθερή θέση και κατασκευάστηκε για να μεταδίδει ένα σταθερό επίπεδο ισχύος. Στη συνέχεια χρησιμοποιήθηκε μια κεραία δέκτη με γνωστό κέρδος για τη μέτρηση της ληφθείσας ισχύος, της πόλωσης και της απόδοσης ισχύος. Η κεραία προέλευσης τοποθετήθηκε σε διάφορες γωνίες κατάδειξης σε σχέση με την κεραία on-chip και διατηρώντας μια σταθερή απόσταση. Αυτή η διαμόρφωση χρησιμοποιήθηκε στο σύστημα μέτρησης κεραίας σταθμών ανιχνευτή, δεδομένου ότι η προτεινόμενη πρωτότυπη κεραία είναι κεραία on-chip και πρέπει να παραμείνει σε σταθερή θέση. Το σύστημα μέτρησης κεραίας με την προσαρτημένη κεραία κόρνας στον δέκτη φαίνεται στο σχήμα 3ένα. Για να μειωθούν οι ανακλάσεις πολλαπλών διαδρομών στο περιβάλλον δοκιμής, εφαρμόστηκε υλικό απορρόφησης ραδιοσυχνοτήτων (RF) σε όλες σχεδόν τις μεταλλικές επιφάνειες και αντικείμενα του σταθμού ανιχνευτή όπως φαίνεται στο Σχ. 3 β. Χρησιμοποιήθηκε αντλία κενού για να συγκρατήσει το τσιπ στον άκαμπτο απορροφητή μικροκυμάτων ενώ ο ανιχνευτής RF έπεσε κάτωΤο Σχ. 3

α ) Το σύστημα μέτρησης κεραίας terahertz με την προσαρτημένη κεραία κόρνας στον δέκτη · και ( β ) Απορροφητικό υλικό RF που φαίνεται ως μαύρο σπογγώδες φύλλο προστέθηκε σε όλες τις επιφάνειες του συστήματος μέτρησης της κεραίας για τη μείωση των αντανακλάσεων πολλαπλών διαδρομών. Η κεραία on-chip τοποθετήθηκε σε έναν άκαμπτο απορροφητή μικροκυμάτων Cascade Microtech και διεγέρθηκε χρησιμοποιώντας τον ανιχνευτή ραδιοσυχνοτήτων γείωσης-σήματος-γείωσης (GSG)Τα προσομοιωμένα και μετρημένα μοτίβα ακτινοβολίας της κεραίας μετα-επιφάνειας on-chip στα 0,41, 0,45 και 0,47 THz φαίνονται στο Σχ. 5 . Τα μετρούμενα αποτελέσματα δείχνουν ότι η κεραία δημιουργεί ένα κατευθυντικό μοτίβο ακτινοβολίας τόσο στο επίπεδο E όσο και στο επίπεδο H και εμφανίζει ένα ευρύ πλάτος δέσμης 3 dB στο εύρος της συχνότητας λειτουργίας του. Αυτό οφείλεται σε ισχυρές ροές ρεύματος στις ανοιχτές γραμμές κουλοχέρηδων που παράγουν ισχυρά πεδία που οδηγούν σε μεγαλύτερο πλάτος δέσμης. Τα αποτελέσματα της προσομοίωσης δείχνουν ότι οι πίσω λοβοί της κεραίας είναι σχετικά μικροί σε σύγκριση με την κύρια δέσμη με αποτέλεσμα υψηλό λόγο εμπρός-πίσω. Δεδομένου ότι το μοτίβο ακτινοβολίας της συμβατικής σχισμής είναι αμφίδρομο, ένας ανακλαστήρας πίσω εφαρμόζεται συχνά για να αποτρέπεται η παρεμβολή της οπίσθιας ακτινοβολίας σε άλλα συστήματα
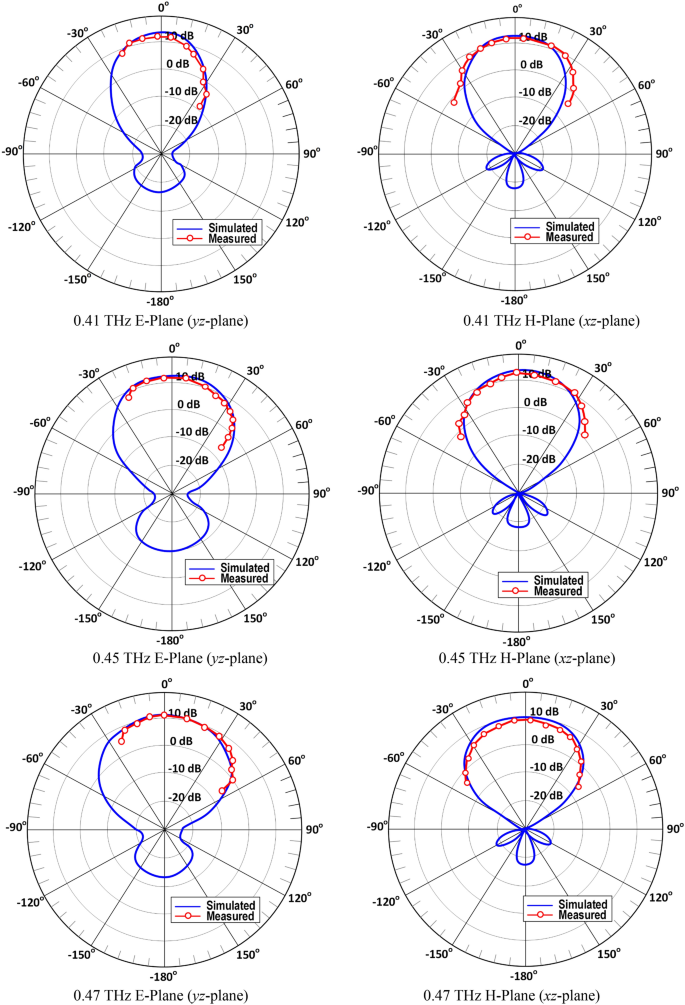
 APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
APOLLO ATLAS CASSINI CERN CMS Curiosity DAWN DNA EINSTEIN FERMI Feynman Hawking Hubble KEPLER LHC LIGO NASA New Horizons NOBEL Opportunity Rosetta Schrödinger VOYAGER ΑΙΝΣΤΑΙΝ ΑΚΤΙΝΕΣ ΓΑΜΑ ΑΝΤΙΥΛΗ ΑΠΟΛΛΩΝ ΑΡΗΣ ΑΣΤΕΡΕΣ ΝΕΤΡΟΝΙΩΝ ΑΣΤΕΡΟΕΙΔΕΙΣ ΑΦΡΟΔΙΤΗ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΓΑΛΑΞΙΑΣ ΓΑΛΑΞΙΕΣ ΓΡΑΦΕΝΙΟ ΔΙΑΣ ΔΙΑΤΤΟΝΤΕΣ ΔΟΡΥΦΟΡΟΙ ΕΓΚΕΦΑΛΟΣ ΕΚΛΕΙΨΗ ΗΛΙΟΥ ΕΠΙΤΑΧΥΝΤΕΣ ΕΡΜΗΣ Η ΑΣΚΗΣΗ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΗΛΕΚΤΡΙΣΜΟΣ ΗΛΙΟΣ ΘΕΩΡΙΑ ΧΟΡΔΩΝ ΚΒΑΝΤΙΚΟΙ ΥΠΟΛΟΓΙΣΤΕΣ ΚΕΠΛΕΡ ΚΟΜΗΤΕΣ ΚΟΣΜΙΚΗ ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ ΚΡΙΜΙΖΗΣ ΚΡΟΝΟΣ ΚΥΜΑΤΑ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΜΕΓΑΛΗ ΕΚΡΗΞΗ ΜΟΝΑΔΕΣ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΝΕΤΡΙΝΟ ΝΟΜΠΕΛ ΟΠΤΙΚΗ ΣΥΣΤΗΜΑ ΠΛΑΝΗΤΕΣ ΠΛΗΘΩΡΙΣΜΟΣ ΠΛΟΥΤΩΝ ΣΕΛΗΝΗ ΣΙΜΟΠΟΥΛΟΣ ΤΑΧΥΤΗΤΑ ΦΩΤΟΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΤΗΛΕΣΚΟΠΙΑ ΤΙΤΑΝΑΣ ΧΡΟΝΟΣ ΧΩΡΟΣ
Subscribe to:
Comments (Atom)