Κβαντικό πείραμα διπλής σχισμής με φωτόνια εμπλεγμένα με ορμή

Το πείραμα σκέψης διπλής σχισμής παρέχει βαθιά εικόνα για την παρέμβαση των κβαντικών σωματιδίων. Αυτή η εργασία παρουσιάζει μια λεπτομερή πειραματική πραγματοποίηση του πειράματος κβαντικής σκέψης διπλής σχισμής με φωτόνια που έχουν εμπλακεί σε ορμή και θεωρητική ανάλυση του πειράματος. Το πείραμα διαμορφώνεται με τέτοιο τρόπο ώστε τα φωτόνια να εμπλέκονται στη διαδρομή και κάθε φωτόνιο να μπορεί να αποκαλύψει τις πληροφορίες πορείας της άλλης φωτονίδας. Κατά συνέπεια, η παρεμβολή ενός φωτονίου καταστέλλεται. Ωστόσο, το μοτίβο παρεμβολών δύο φωτονίων εμφανίζεται εάν οι θέσεις ανίχνευσης των φωτονίων συσχετίζονται χωρίς να αποκαλύπτονται οι πληροφορίες πορείας ποιας σχισμής. Αποδεικνύεται επίσης πειραματικά και θεωρητικά ότι η κβαντική παρεμβολή δύο φωτονίων εξαφανίζεται όταν ανιχνεύεται η πορεία κοπής ενός φωτονίου στη διπλή σχισμή. Εισαγωγή Η κυματική φύση του φωτός αποδείχθηκε αρχικά πειραματικά με το πείραμα 1 , 2 του διάσημου Young . Στην κβαντική φυσική, το φως κβαντοποιείται με τη μορφή κβαντικής ενέργειας γνωστής ως φωτονίου. Σύμφωνα με τη δήλωση του PAM Dirac, «Κάθε φωτονίο παρεμβαίνει μόνο στον εαυτό του» 3 . Αυτή η μόνη παρέμβαση ενός φωτονίου είναι συνέπεια της αρχής της κβαντικής υπέρθεσης. Εάν τα φωτόνια εμφανίζονται σε μια διπλή σχισμή ένα προς ένα, τότε το μοτίβο παρεμβολής ενός φωτονίου εμφανίζεται σταδιακά. Όπου η ανίχνευση κάθε φωτονίου αντιστοιχεί σε ένα σημείο στην οθόνη. Το πείραμα Double-slit του Young παρέχει βαθιά εικόνα για τη δυαδικότητα των κυμάτων-σωματιδίων εάν είναι φανταστικό για μεμονωμένα σωματίδια 4. Το μοτίβο παρεμβολής ενός μεμονωμένου σωματιδίου δεν σχηματίζεται εάν είναι γνωστές οι πληροφορίες διαδρομής ενός σωματιδίου, δηλαδή μια σχισμή μέσω της οποίας έχει περάσει ένα σωματίδιο. Σύμφωνα με την ερμηνεία της Κοπεγχάγης, μια παρατήρηση σχετικά με την κβαντική υπέρθεση των διαδρομών ενός σωματιδίου αντιστοιχεί σε μια μέτρηση που καταρρέει την κβαντική υπέρθεση, επομένως, δεν σχηματίζεται μοτίβο παρεμβολών. Από την άλλη πλευρά, τι συμβαίνει εάν τροποποιήσουμε το πείραμα με τέτοιο τρόπο ώστε οι πληροφορίες πορείας ενός σωματιδίου να μην είναι διαθέσιμες κατά τη διέλευσή του μέσω διπλής σχισμής, αλλά μπορούν να ληφθούν ακόμη και μετά την ανίχνευσή του. Σε αυτήν την περίπτωση, η πορεία πορείας μπορεί να πραγματοποιηθεί από την κβαντική κατάσταση ενός άλλου σωματιδίου εάν η συνολική κβαντική κατάσταση των σωματιδίων είναι μια εμπλεγμένη κβαντική κατάσταση. Γνωρίζοντας την πορεία του με μια μέτρηση, προσδιορίζεται αμέσως η πληροφορία διαδρομής του άλλου σωματιδίου. Λόγω της διαδρομής που αποκαλύπτει την κβαντική εμπλοκή των σωματιδίων, καταστέλλεται η παρεμβολή μεμονωμένων σωματιδίων. Ωστόσο, η κβαντική παρεμβολή μπορεί να ανακτηθεί ακόμα και μετά την ολοκλήρωση του πειράματος κάνοντας συσχετισμένη επιλογή των αποτελεσμάτων της μέτρησης. Το πρώτο πείραμα που έδειξε την παρεμβολή του φωτός με πολύ χαμηλή ένταση στο πείραμα Young-double-slit πραγματοποιήθηκε το 1909 από τον GI Taylor 5 . Ενδιαφέροντα πειράματα που δείχνουν τις παρεμβολές διπλής σχισμής του Young εκτελούνται με νετρόνια από τη θεμελιώδη προοπτική της κβαντικής μηχανικής 6 , με δέσμες ηλεκτρονίων 7 και με ένα μόνο ηλεκτρόνιο που διέρχεται από μια διπλή σχισμή 8 , 9 , 10 . Πρόσφατα, αναφέρθηκε μια πρώτη πειραματική επίδειξη παρεμβολής αντισωμάτων με διπλή σχισμή 11 . Η παρέμβαση των μακρομορίων είναι το αντικείμενο μεγάλου ενδιαφέροντος για την αναζήτηση της κβαντικής υπέρθεσης μεσοσκοπικών και μακροσκοπικών αντικειμένων12 , 13 . Σε αυτό το πλαίσιο, έχουν πραγματοποιηθεί πολλά ενδιαφέροντα πειράματα για να παραχθεί μια υπέρθεση διαδρομής μεγάλων μορίων παρόμοια με τα πειράματα παρεμβολής τύπου διπλής σχισμής 14 , 15 , 16 . Η κύρια ιδέα ενός πειράματος κβαντικής μονής διπλής σχισμής επεκτάθηκε σε ένα κβαντικό πείραμα διπλής σχισμής με σκέψη Greenberger, Horne και Zeilinger 17 για να παρέχει θεμελιώδη εικόνα σχετικά με την κβαντική παρέμβαση πολλαπλών σωματιδίων. Στο χαρτί τους. έχουν εξετάσει δύο διπλές σχισμές και μια πηγή σωματιδίων που τοποθετούνται στη μέση των διπλών σχισμών. Κάθε σωματίδιο ανιχνεύεται ξεχωριστά αφού διασχίζει μια διπλή σχισμή. Η κβαντική εμπλοκή σωματιδίων εμφανίζεται φυσικά στις εκτιμήσεις τους 18 , 19και φαίνεται, όταν εξαφανίζονται οι παρεμβολές ενός μορίου και εμφανίζονται δύο παρεμβολές. Μια πειραματική πραγματοποίηση κβαντικού πειράματος με διπλή σχισμή που δείχνει παρεμβολή δύο φωτονίων έχει αποδειχθεί με κβαντικά συσχετισμένα φωτόνια που παράγονται με διαδικασία αυθόρμητης παραμετρικής μετατροπής (SPDC) 20. Ωστόσο, σε αυτό το άρθρο, παρουσιάζουμε μια λεπτομερή πειραματική πραγματοποίηση του πειράματος κβαντικής σκέψης διπλής σχισμής με ζεύγη φωτονίων που έχουν εμπλακεί σε ορμή, όπου πραγματοποιείται μια εικονική διαμόρφωση διπλής σχισμής με δύο διπρισμούς Fresnel. Αυτή η εργασία παρέχει μια λεπτομερή εννοιολογική, θεωρητική και πειραματική ανάλυση του κβαντικού πειράματος διπλής σχισμής. Επιπλέον, παρουσιάζεται ένα πείραμα ανίχνευσης πορείας πορείας φωτονίου όπου αποδεικνύεται ότι η παρεμβολή δύο φωτονίων εξαφανίζεται όταν ανιχνεύεται πορεία κοπής φωτονίου. Σε αυτό το άρθρο, τα πειράματα παρουσιάζονται στο πλαίσιο ενός πειράματος κβαντικής σκέψης διπλής σχισμής. Εντούτοις, μελετήθηκαν εντατικά πειράματα θεμελιώδους σημασίας με τα εμπλεκόμενα στην πόλωση φωτονία 21 , 22 , 23 και τα ορμονικά εμπλεκόμενα φωτόνια 24 . Επιπλέον, ενδιαφέροντα πειράματα σχετικά με τη διαγραφή καθυστερημένης επιλογής διαδρομής 25 , 26 , 27 , 28 , 29 , 30 και παρεμβολών δύο φωτονίων 31 , 32 , 33 , 34 , 35 , 36 , 37 ,Πραγματοποιούνται 38 , 39 , 40 . Παρόμοια πειράματα έχουν προταθεί με το Einstein – Podolsky – Rosen (EPR) εμπλεγμένο ζευγάρι ατόμων 41 .>>>>>>Κβαντικό πείραμα διπλής σχισμήςο κβαντικό πείραμα διπλής σχισμής αποτελείται από δύο διπλές σχισμές και μια πηγή ζευγών φωτονίων. Σε αυτήν την πειραματική κατάσταση, ένα μόνο φωτόνιο διέρχεται από κάθε διπλή σχισμή και ανιχνεύεται ξεχωριστά σε οθόνες τοποθετημένες πίσω από τις διπλές σχισμές, όπως φαίνεται στο Σχ. 1 . Ωστόσο, η παρέμβαση των φωτονίων εξαρτάται από την κβαντική κατάσταση των δύο φωτονίων. Για να κατανοήσετε την κβαντική παρεμβολή δύο φωτονίων σε ένα πείραμα με διπλή σχισμή, λάβετε υπόψη ότι μια πηγή παράγει φωτόνια σε ζεύγη και και τα δύο φωτόνια έχουν την ίδια γραμμική πόλωση. Η διπλή σχισμή 1 και η διπλή σχισμή 2 ευθυγραμμίζονται παράλληλα με τον άξονα y και τοποθετούνται σε αποστάσεις και , αντίστοιχα κατά μήκος του άξονα x από την πηγή. Μονές σχισμές μεγάλο 1 μεγάλο 2 a_ {1} b_ {1} D_ {1} a_ {2} b_ {2} D_ {2} s_ {1} s_ {2} o_ {1} o_ {2} a_ { 1} a_ {2} b_ {1} b_ {2} a_ {1} b_ {2} b_ {1} a_ {2} a_ {12} o_ {1} o_ {2} ένα 1 και της διπλής σχισμής 1 διαχωρίζονται με απόσταση και μεμονωμένες σχισμές και της διπλής σχισμής 2 διαχωρίζεται με απόσταση όπως φαίνεται στο Σχ. 1 όπου κάθε πλάτος σχισμής θεωρείται ότι είναι άπειρα μικρό. Στην οθόνη 1 ανιχνεύεται ένα μοναδικό φωτόνιο ζεύγους φωτονίων, το οποίο είναι τοποθετημένο σε απόσταση από τη διπλή σχισμή 1 και ένα δεύτερο φωτόνιο ανιχνεύεται στην οθόνη 2, η οποία βρίσκεται σε απόσταση από διπλή σχισμή 2. Υπάρχουν τέσσερις διαφορετικές πιθανές διαδρομές με τις οποίες μπορούν να φτάσουν τα φωτόνια στις αντίστοιχες οθόνες, δηλαδή ένα φωτόνιο μπορεί να φτάσει σε ένα σημείο σι 1 ρε 1 ένα 2 σι 2 ρε 2 μικρό 1 μικρό 2 ο 1 στην οθόνη 1 μέσω διπλής σχισμής 1 και το άλλο φωτόνιο μπορεί να φτάσει σε ένα σημείο στην οθόνη 2 μέσω διπλής σχισμής 2. Επομένως, πιθανές διαδρομές φωτονίων είναι ( i) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (ii) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (iii) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ή (iv) ένα πρώτο φωτόνιο μπορεί να περάσει από σχισμή και το δεύτερο φωτόνιο μπορεί να περάσει από σχισμή ο 2 ένα 1 ένα 2 σι 1 σι 2 ένα 1 σι 2 σι 1 ένα 2 . Δεδομένου ότι όλες οι πιθανές διαδρομές δεν είναι διακριτές και δεν αποκαλύπτουν πληροφορίες πορείας, επομένως, συνολικό πλάτος για να βρείτε ένα φωτόνιο στο και ένα φωτόνιο στο μαζί είναι μια κβαντική υπέρθεση όλων των πιθανών διαδρομών, οι οποίες μπορούν να γραφτούν διαδοχικά ως ΕΝΑ 12 ο 1 ο 2 ΕΝΑ 12 = ⟨ ο 2 | ένα 2 ⟩ τ ένα 2 ⟨ ένα 2 | ⟨ ο 1 | ένα 1 ⟩ τ ένα 1 ⟨ ένα 1 | ψ ⟩ + ⟨ ο 2 | σι 2 ⟩ τ σι 2 ⟨ σι 2 | ⟨ ο 1 | σι 1 ⟩ τ σι 1 ⟨ σι 1 | ψ ⟩ + ⟨ ο 2 | σι 2 ⟩ τ σι 2 ⟨ σι 2 | ⟨ ο 1 | ένα 1 ⟩ τ ένα 1 ⟨ ένα 1 | ψ ⟩ + ⟨ ο 2 | ένα 2 ⟩ τ ένα 2 ⟨ ένα 2 | ⟨ ο 1 | σι 1 ⟩ τ σι 1 ⟨ σι 1 | ψ ⟩ (1) όπου , , , είναι πλάτη μετάδοσης σχισμών , , , , αντίστοιχα. Οι κβαντικές καταστάσεις , , είναι θέση διαστημικές βάσεις καταστάσεις θέσεων στις σχισμές σε διπλή σχισμή 1 και διπλή σχισμή 2, αντίστοιχα όπου μπορεί να βρεθεί ένα φωτόνιο Ομοίως, και τ ένα 1 τ σι 1 τ ένα 2 τ σι 2 ένα 1 σι 1 ένα 2 σι 2 | ένα 1 ⟩ | σι 1 ⟩ | ένα 2 ⟩ | σι 2 ⟩ | ο 1 ⟩ | ο 2 ⟩ είναι οι καταστάσεις βάσης θέσης θέσης των τοποθεσιών στις οθόνες. Ωστόσο, οι καταστάσεις βάσης θέσης που αντιστοιχούν σε σημεία σε κάθε διπλή σχισμή και μια οθόνη σχηματίζουν ένα διαφορετικό σύνολο βάσεων έτσι ώστε αντιπροσωπεύει το πλάτος του μεταδιδόμενου φωτονίου που πηγαίνει από τη σχισμή σε μια τοποθεσία στην οθόνη 1. Η ίδια ορολογία εφαρμόζεται για άλλα πλάτη στην Εξ. 1 . ⟨ ο 1 | ένα 1 ⟩ ένα 1 ο 1 Φιγούρα 
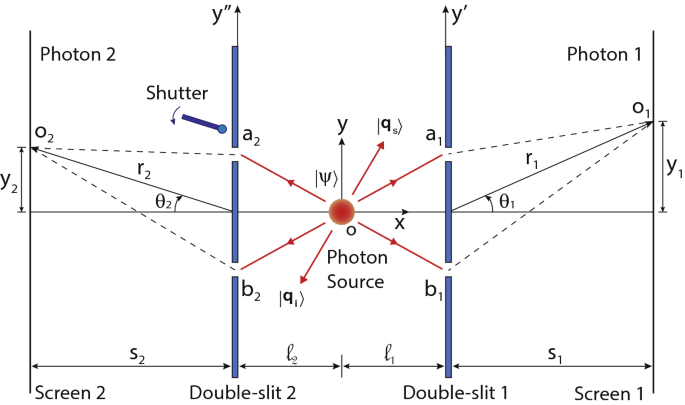
Ένα σχηματικό διάγραμμα ενός πειράματος με διπλή σχισμή. Τα φωτόνια ανιχνεύονται ξεχωριστά σε οθόνες αφού περάσουν ξεχωριστά από τις διπλές σχισμές. Πληροφορίες πορείας πορείας με σχισμή των φωτονίων μπορούν να ανιχνευθούν αποκλείοντας οποιαδήποτε μεμονωμένη σχισμή κλείνοντας το κλείστροΠεραιτέρω, θεωρήστε ότι τα ζεύγη φωτονίων που παράγονται από μια πηγή πεπερασμένου μεγέθους εκπέμπονται σε αντίθετες κατευθύνσεις μεταξύ τους έτσι ώστε να εμπλέκονται η ορμή, η καθαρή ορμή τους είναι μηδέν και η ορμή κάθε φωτονίου είναι σίγουρα άγνωστη. Λάβετε υπόψη ότι η χωρική επέκταση της πηγής είναι πολύ μικρότερη από τον διαχωρισμό των σχισμών, αλλά είναι μεγάλη για την παραγωγή ορμής εμπλοκής. Ως συνέπεια της εμπλοκής της ορμής, εάν ένα φωτόνιο διέρχεται από σχισμή τότε το άλλο φωτόνιο διέρχεται από σχισμή και εάν ένα φωτόνιο διέρχεται από σχισμή έπειτα το άλλο φωτόνιο περνάει από τη σχισμή ένα 1 σι 2 σι 1 ένα 2 μετά τη μετάδοσή τους μέσω των σχισμών. Για τα φωτόνια που εμπλέκονται στην ορμή, και οι δύο αυτές δυνατότητες είναι κβαντικές υπερτιθέμενες, με αποτέλεσμα και τα δύο φωτόνια να εμπλέκονται στη διαδρομή μέσω των σχισμών και των δύο πρώτων όρων στην άθροιση του Εξ. 1 γίνεται μηδέν. Οι δύο τελευταίοι όροι στο άθροισμα οφείλονται στην εμπλοκή της διαδρομής μέσω των σχισμών, αυτά τα δύο πλάτη αλληλεπιδρούν μεταξύ τους και παράγουν παρεμβολή δύο-φωτονίων των εμπλεκόμενων με ορμή φωτονίων. Όταν ανοίγουν και οι τέσσερις σχισμές, δεν αποκαλύπτονται πληροφορίες διαδρομής δύο φωτονίων και μπορεί να παρατηρηθεί παρεμβολή δύο φωτονίων με καταγραφή θέσεων ανίχνευσης ενός φωτονίου που αντιστοιχεί σε μια συγκεκριμένη θέση ανίχνευσης άλλου φωτονίου στην άλλη οθόνη κατά τη διάρκεια κάθε επανάληψης το πείραμα. Από την άλλη πλευρά, εάν κάποιος μετρήσει την κατεύθυνση της ορμής οποιουδήποτε μεμονωμένου φωτονίου πριν από τη διέλευση του μέσω διπλών σχισμών, τότε η κατάσταση εμπλοκής της ορμής καταρρέει. Αυτό το αποτέλεσμα της μέτρησης αποκαλύπτει την κατεύθυνση ορμής ενός φωτονίου στο οποίο πραγματοποιείται μια μέτρηση και η κατεύθυνση της ορμής του άλλου φωτονίου αποκαλύπτεται επίσης αμέσως μετά την κατάρρευση ακόμη και χωρίς να γίνει καμία μέτρηση σε αυτό. Αυτή η μέτρηση αποκαλύπτει ποια διαδρομή διαδρομής των φωτονίων. Από την άλλη πλευρά, ποια διαδρομή σχισμών των φωτονίων στη διπλή σχισμή μπορεί να ανιχνευθεί κλείνοντας οποιαδήποτε μεμονωμένη σχισμή με κλείστρο. Ένα κλείστρο που φαίνεται στο Σχ. 1 θεωρείται ανιχνευτής μέτρησης φωτονίων, εάν το κλείστρο είναι κλειστό για να μπλοκάρει μια σχισμή ένα 2 και ένα φωτόνιο ανιχνεύεται στην οθόνη 2 και στη συνέχεια αποκαλύπτει ότι ένα φωτόνιο περνάει από μια σχισμή λόγω της κατάρρευσης της κβαντικής εμπλοκής κατάστασης που προκαλείται από τον ανιχνευτή κλείστρου. Κατά συνέπεια, μπορεί κανείς να ανακαλύψει ότι το άλλο φωτόνιο περνάει από μια σχισμή εάν εντοπιστεί στο σι 2 ένα 1 ο 1 . Δεδομένου ότι είναι γνωστή μια διαδρομή και των δύο φωτονίων, η παρεμβολή δύο φωτονίων καταστέλλεται. Ενδιαφέρουσα κατάσταση εμφανίζεται όταν οι διπλές σχισμές 2 και η οθόνη 2 αφαιρούνται για να επιτρέψουν σε ένα φωτόνιο να διαδίδεται στο διάστημα ενώ άλλο φωτονίο περνά μέσω της διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1. Μια παρέμβαση ενός φωτονίου δεν παράγεται στην οθόνη 1 λόγω διαδρομής εμπλοκή της πορείας πορείας των φωτονίων μπορεί να ληφθεί μετρώντας την ορμή του φωτονίου διάδοσης ακόμη και μετά την ανίχνευση ενός φωτονίου στην οθόνη 1. Επιπλέον, όταν ανοίγονται όλες οι σχισμές και δεν εντοπίζεται ποια σχισμή, ένα φωτόνιο μπορεί να ανιχνευθεί σε οποιαδήποτε θέση σε μια οθόνη τυχαία κατά τη διάρκεια κάθε επανάληψης του πειράματος και η θέση ανίχνευσής του δεν είναι γνωστή πριν από μια μέτρηση στην οθόνη. Μόλις ένα φωτονίο ανιχνευθεί σε μια οθόνη, η θέση ανίχνευσής του καθορίζει αμέσως το πλάτος για να βρει άλλο φωτονίο σε άλλη οθόνη εάν δεν επιτευχθεί εκεί. Τα μεμονωμένα φωτόνια δεν εμφανίζουν παρεμβολές στην οθόνη επειδή ένα καλά καθορισμένο εύρος συνεκτικής φάσης για την εύρεση ενός φωτονίου στην οθόνη εξαρτάται από μια συγκεκριμένη θέση ανίχνευσης άλλων φωτονίων. Σε αυτήν την περίπτωση, ένα πλάτος ενός φωτονίου είναι εντελώς ασυνεπές. Οι πληροφορίες για τη θέση ανίχνευσης ενός φωτονίου καθορίζουν ένα συγκεκριμένο μοτίβο παρεμβολών δύο φωτονίων. Με άλλα λόγια, σε αυτόν τον τύπο κοινής και συσχετισμένης καταχώρησης θέσεων ανίχνευσης φωτονίων, εάν επιλεγεί διαφορετική θέση ανίχνευσης ενός φωτονίου, το μοτίβο παρεμβολών δύο φωτονίων παρουσιάζει μετατόπιση. Εάν καταγράφονται μόνο μεμονωμένα φωτόνια σε κάθε οθόνη χωρίς να υπάρχει συσχέτιση μεταξύ των θέσεων ανίχνευσής τους, τότε το μοτίβο παρεμβολών δεν σχηματίζεται σε κάθε οθόνηΠαρεμβολή δύο φωτονίων...Για να μάθετε μια παρέμβαση δύο φωτονίων στο πείραμα double-double-slit για ένα πεπερασμένο πλάτος κάθε σχισμής, λάβετε υπόψη ότι μια πηγή φωτονίων που βρίσκεται στην προέλευση παράγει μια κβαντική κατάσταση δύο φωτονίων ως φαίνεται στο Σχ. 1 . Οι διπλές σχισμές μπορούν να οριστούν από τις λειτουργίες μετάδοσης πλάτους και της διπλής σχισμής 1 και της διπλής σχισμής 2 αντίστοιχα. Όπου και είναι τα αυθαίρετα σημεία στη διπλή σχισμή 1 και τη διπλή σχισμή 2, αντίστοιχα έτσι ώστε η βάση θέσης να αντιστοιχεί σε αυτά τα σημεία που βρίσκονται στις διπλές σχισμές όπου ένα φωτόνιο μπορούν να βρεθούν είναι και | Ψ ⟩ t_ {1} (y ') t_ {2} (y ") y" y " | l_ {1}, y" \ rangle | l_ {2}, y "\ rangle A_ { 12} o_ {1} o_ {2} τ 1 ( ε ′ ) τ 2 ( ε ′ ′ ) ε ′ ε ′ ′ | μεγάλο 1 , ε ′ ⟩ | μεγάλο 2 , ε ′ ′ ⟩ . Επομένως, το εύρος για εύρεση φωτονίων στα σημεία και μαζί στις οθόνες μπορεί να γραφτεί ως ΕΝΑ 12 ο 1 ο 2 ΕΝΑ 12 = ∫ ∞ - ∞ ∫ ∞ - ∞ ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ τ 2 ( ε ′ ′ ) ⟨ μεγάλο 2 , ε ′ ′ | ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ τ 1 ( ε ′ ) ⟨ μεγάλο 1 , ε ′ | Ψ ⟩ ρε ε ′ ρε ε ′ ′ (2) Ας υποθέσουμε ότι η πηγή φωτονίων έχει πεπερασμένο μέγεθος και η κβαντική κατάσταση δύο φωτονίων είναι μια κβαντική κατάσταση εμπλεκόμενη στην ορμή, όπου και τα δύο φωτόνια έχουν την ίδια γραμμική πόλωση και συχνότητα. Μια τέτοια κβαντική κατάσταση εμπλοκής δύο φωτονίων μπορεί να παραχθεί από εκφυλισμένο μη γραμμικό SPDC με αντιστοίχιση φάσης τύπου Ι σε κρύσταλλο βήτα-βορικού βορικού (BBO) ο οποίος αντλείται από μια ακτίνα λέιζερ που διαδίδεται κατά μήκος του z- άξονα (διαμήκη κατεύθυνση), όπου το z- άξονας (δεν φαίνεται στο Σχ. 1 ) είναι κάθετο προς το xy | Ψ ⟩ -πλάνο (εγκάρσιο επίπεδο). Τα φωτόνια που είναι γνωστά ως το σήμα και τα αδρανή φωτόνια εκπέμπονται από την πηγή με αντίθετη ροπή με σχεδόν ίσο μέγεθος στο εγκάρσιο επίπεδο έτσι ώστε η κατάσταση εμπλοκής των δύο-φωτονίων στο χώρο της εγκάρσιας ορμής να είναι 42 , 43 , 44 , 45 , 46 | Ψ ⟩ = Ν ∫ ∫ ρε ε μικρό ρε ε Εγώ Φ ( ε μικρό , ε Εγώ ) | ε μικρό ⟩ | ε Εγώ ⟩ (3) όπου , είναι οι εγκάρσιες κβαντικές καταστάσεις ορμής του σήματος και τα αδρανή φωτόνια της ορμής και , αντίστοιχα και το Ν είναι μια σταθερά κανονικοποίησης. κύματος δύο φωτονίων αντιπροσωπεύει το εύρος για την εύρεση ενός φωτονίου σήματος σε κατάσταση ορμής και ένα αδρανές φωτόνιο σε κατάσταση ορμής . Η κβαντική εμπλοκή εκδηλώνεται από τη μη διαχωρισσιμότητα των | ε μικρό ⟩ | ε Εγώ ⟩ ε μικρό ε Εγώ \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}}}) | \ mathbf {q_ {s}} \ rangle | \ mathbf {q_ {i}} \ rangle \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}} }) \ Phi (\ mathbf {q_ {s}, \ mathbf {q_ {i}}}) Φ ( ε μικρό , ε Εγώ ) | ε μικρό ⟩ | ε Εγώ ⟩ Φ ( ε μικρό , ε Εγώ ) . Για την ακτίνα λέιζερ της αντλίας με προφίλ έντασης gaussian πεπερασμένου πλάτους στο εγκάρσιο επίπεδο, η δύο φωτονίων είναι εμφανής μόνο για καταστάσεις ορμής των φωτονίων με αντίθετη εγκάρσια ροπή. Δεδομένου ότι το μέγεθος της πηγής είναι πεπερασμένο, εάν η ορμή ενός φωτονίου μετριέται ακριβώς τότε η κβαντική κατάσταση του άλλου φωτονίου αντιστοιχεί σε μια κατάσταση ορμής αντίθετης ορμής με πεπερασμένη αβεβαιότητα. Περαιτέρω λεπτομέρειες σχετικά με την ορμή εμπλοκής των φωτονίων που παράγονται από εκφυλισμένο μη γραμμικό SPDC στον κρύσταλλο BBO δίδονται με μεθόδους. Φ ( ε μικρό , ε Εγώ ) Υπάρχουν δύο δυνατότητες που μπορούν να οδηγήσουν σε από κοινού ανίχνευση φωτονίων στην οθόνη 1 και στην οθόνη 2. Αυτές οι διακριτές δυνατότητες είναι (i) το φωτονίο σήματος διέρχεται μέσω διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1 και το αδρανές φωτόνιο διέρχεται μέσω διπλού - slit 2 και ανιχνεύεται στην οθόνη 2 και (ii) το αδρανές φωτόνιο διέρχεται μέσω της διπλής σχισμής 1 και ανιχνεύεται στην οθόνη 1 και το φωτονίο σήματος διέρχεται μέσω της διπλής σχισμής 2 και ανιχνεύεται στην οθόνη 2. Οποιοδήποτε μεμονωμένο φωτόνιο (σήμα ή idler) που μπορεί να ανιχνευθεί αφού περάσει από τη διπλή σχισμή 1 επισημαίνεται ως φωτόνιο 1 και οποιοδήποτε μεμονωμένο φωτόνιο που μπορεί να ανιχνευθεί μετά τη διέλευση από τη διπλή σχισμή 2 επισημαίνεται ως φωτόνιο 2. Το φωτόνιο 1 και το φωτόνιο 2 δεν μπορούν να διακριθούν καθώς έχουν την ίδια συχνότητα και πόλωση. Εξετάστε, η λειτουργία μετάδοσης της διπλής σχισμής 1 είναι τ 1 ( ε ′ ) = ένα ′ τ ( μι - ( ε ′ - ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 + μι - ( ε ′ + ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 ) , που αντιπροσωπεύει δύο γκάους σχισμές με διαχωρισμό μεταξύ τους και πλάτος σχισμής κάθε σχισμής είναι τέτοιο που είναι σημαντικά μεγαλύτερο από το . Παρομοίως, η λειτουργία μετάδοσης της διπλής σχισμής 2 είναι , ρε 1 σ 1 ρε 1 σ 1 τ 2 ( ε ′ ′ ) = ένα ′ ′ τ ( μι - ( ε ′ ′ - ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 + μι - ( ε ′ ′ + ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 ) ρε 2 σ 2 κάθε σχισμής είναι τέτοιο που είναι σημαντικά μεγαλύτερο από το . Όπου, και είναι οι σύνθετοι πολλαπλασιαστές των λειτουργιών μετάδοσης, περιλαμβάνουν τη μετατόπιση φάσης που εισάγεται από τις σχισμές και περιορίζει τη μέγιστη μετάδοση σε μία. Για , η μετάδοση των σχισμών είναι μηδέν. Κάθε διπλή σχισμή τοποθετείται πολύ μακριά από την πηγή σε σύγκριση με τον διαχωρισμό των σχισμών. Επομένως, οι σχισμές βρίσκονται σε στενή κλίση με το x ρε 2 σ 2 ένα ′ τ ένα ′ ′ τ ένα ′ τ = ένα ′ ′ τ = 0 - άξονας έτσι ώστε τα φωτόνια που προέρχονται από την πηγή να εμφανίζονται σε σχισμές σχεδόν κοντά στην κανονική συχνότητα. Για να έχει εμπλοκή διαδρομής δύο φωτονίων μέσω των σχισμών, οι διπλές σχισμές είναι τοποθετημένες έτσι ώστε και . Επιπλέον, η αβεβαιότητα της συνιστώσας ορμής κάθε φωτονίου παράλληλη με τις διπλές σχισμές, υπό την προϋπόθεση ότι η ορμή του άλλου φωτονίου προσδιορίζεται με ακρίβεια, είναι τόσο μικρή ώστε για την καταστολή της παρεμβολής ενός φωτονίου από κάθε διπλή σχισμή, όπου q είναι το μέγεθος της ορμής ενός φωτονίου 41 . Ωστόσο, ρε 1 / μεγάλο 1 = ρε 2 / μεγάλο 2 σ 1 / μεγάλο 1 = σ 2 / μεγάλο 2 Δ ε ∥ Δ ε ∥ / ε ≪ ρε 1 / μεγάλο 1 = ρε 2 / μεγάλο 2 Δ ε ∥ / ε ≈ σ 1 / μεγάλο 1 = σ 2 / μεγάλο 2 . Αυτές οι συνθήκες υπονοούν, εάν ένα φωτόνιο διέρχεται μέσω σχισμής τότε το άλλο φωτονίο περνά πιθανότατα μέσω σχισμής και εάν ένα φωτόνιο διέρχεται μέσω σχισμής το άλλο φωτόνιο πιθανότατα περνάει από τη σχισμή . Επομένως, τα φωτόνια που συμβάλλουν στην ανίχνευση αρθρώσεων στις οθόνες εμπλέκονται μέσω των σχισμών. Ωστόσο, εάν ένα φωτόνιο απορροφάται πολύ μακριά από σχισμές σε αυθαίρετη θέση στη διπλή σχισμή 1, τότε το άλλο φωτόνιο πιθανότατα απορροφάται στο ένα 1 σι 2 σι 1 ένα 2 ε ′ ε ′ ′ = - ε ′ μεγάλο 2 / μεγάλο 1 πολύ μακριά από σχισμές διπλής σχισμής 2. Η μετάδοση κάθε σχισμής θεωρείται γκάους με πολύ μικρό πλάτος που επιτρέπει σε ένα φωτόνιο να περάσει μέσα από αυτό. Υπό αυτές τις εκτιμήσεις, το εύρος της κοινής ανίχνευσης των φωτονίων στις οθόνες λαμβάνει σημαντική συνεισφορά από ένα μικρό εύρος καταστάσεων ορμής της κβαντικής κατάστασης . Οι υπόλοιπες καταστάσεις ορμής στο απορροφώνται σε διπλές σχισμές. Επομένως, για να αξιολογήσετε χρησιμοποιώντας το Εξ. 2 , μπορεί να εφαρμοστεί μια ακόλουθη προσέγγιση ΕΝΑ 12 | Ψ ⟩ | Ψ ⟩ ΕΝΑ 12 τ 2 ( ε ′ ′ ) τ 1 ( ε ′ ) ⟨ μεγάλο 2 , ε ′ ′ | ⟨ μεγάλο 1 , ε ′ | Ψ ⟩ ≈ ένα ′ ′ τ ένα ′ τ ντο β ( μι Εγώ ε ( ρ ένα 1 + ρ σι 2 ) / ℏ ⋅ μι - ( ε ′ - ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 μι - ( ε ′ ′ + ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 + μι Εγώ ε ( ρ σι 1 + ρ ένα 2 ) / ℏ ⋅ μι - ( ε ′ + ρε 1 / 2 ) 2 / 2 σ 2 1 ( 2 π ) 1 / 2 σ 1 μι - ( ε ′ ′ - ρε 2 / 2 ) 2 / 2 σ 2 2 ( 2 π ) 1 / 2 σ 2 ) (4) όπου είναι μια σταθερά αναλογικότητας που εξαρτάται από τη λειτουργία κύματος δύο φωτονίων. Δεδομένου ότι τα φωτόνια εμφανίζονται σε κάθε σχισμή κοντά στην κανονική συχνότητα εμφάνισης, το είναι το πλάτος δύο φωτονίων ενός φωτονίου για μετάβαση από την πηγή για σχισμή βρίσκεται σε απόσταση και άλλο φωτονίο για μετάβαση από την πηγή στη σχισμή βρίσκεται σε απόσταση . Παρομοίως, το είναι το πλάτος δύο φωτονίων ενός φωτονίου για μετάβαση από την πηγή στην σχισμή βρίσκεται στο μια απόσταση και άλλα φωτόνια για μετάβαση από την πηγή στη σχισμή ντο β μι Εγώ ε ( ρ ένα 1 + ρ σι 2 ) / ℏ ένα 1 ρ ένα 1 σι 2 ρ σι 2 μι Εγώ ε ( ρ σι 1 + ρ ένα 2 ) / ℏ σι 1 ρ σι 1 ένα 2 r_ {a2} a_ {1} a_ {2} b_ {1} b_ {2} \ Phi (\ mathbf {q_ {s} , \ mathbf {q_ {i}}}) βρίσκεται σε απόσταση . Το μεταδιδόμενο πλάτος των φωτονίων μέσω των σχισμών και ή μέσω των σχισμών και είναι αμελητέο επειδή είναι πολύ μικρό για αυτές τις διαδρομές. Τα φωτόνια εμπλέκονται μέσω των σχισμών και της εξίσωσης. 4 αντιπροσωπεύει το πλάτος των μεταδιδόμενων φωτονίων στις διπλές σχισμές που οδηγούν στην κοινή ανίχνευση των φωτονίων. ρ ένα 2 ένα 1 ένα 2 σι 1 σι 2 Φ ( ε μικρό , ε Εγώ ) Το μεταδιδόμενο πλάτος φωτονίου ενός φωτονίου προέρχεται περαιτέρω από ένα σημείο σε μια διπλή σχισμή έτσι ώστε να αντιστοιχεί σε μια ομοιόμορφη κατανομή πιθανότητας του φωτονίου που βρίσκεται στην οθόνη. Τα πλάτη των μεταδιδόμενων φωτονίων για μετάβαση από μια θέση σημείου σε μια διπλή σχισμή σε μια θέση σημείου στην πλησιέστερη οθόνη είναι και για το φωτόνιο 1 και το φωτόνιο 2, αντίστοιχα. Όπου και είναι οι αποστάσεις και από αυθαίρετα σημεία και ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ ∝ μι Εγώ ε | Ρ ′ | / ℏ / | Ρ ′ | 1 / 2 ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ ∝ μι Εγώ ε | Ρ ′ ′ | / ℏ / | Ρ ′ ′ | 1 / 2 Ρ ′ Ρ ′ ′ ο 1 ο 2 ε ′ ε ′ ′ βρίσκεται σε διπλή σχισμή 1 και διπλή σχισμή 2, αντίστοιχα. Δεδομένου ότι οι αποστάσεις και των οθονών από τις πλησιέστερες διπλές σχισμές είναι πολύ μεγαλύτερες από τις διαχωριστικές σχισμές, επομένως, και , όπου και είναι οι αποστάσεις και από τα μεσαία σημεία της διπλής σχισμής 1 και της διπλής σχισμής 2, αντίστοιχα όπως φαίνεται στο Σχ. 1 . Μετά την επίλυση Εξ. 2 μικρό 1 μικρό 2 ⟨ ο 1 | μεγάλο 1 , ε ′ ⟩ ∝ μι Εγώ ε ( ρ 1 - ε ′ αμαρτία ( θ 1 ) ) / ℏ / ρ 1 / 2 1 ⟨ ο 2 | μεγάλο 2 , ε ′ ′ ⟩ ∝ μι Εγώ ε ( ρ 2 - ε ′ ′ αμαρτία ( θ 2 ) ) / ℏ / ρ 1 / 2 2 ρ 1 ρ 2 ο 1 ο 2 χρησιμοποιώντας το Εξ. 4 το εύρος της κοινής ανίχνευσης των φωτονίων μπορεί να γραφτεί ως ΕΝΑ 12 = ντο ν μι Εγώ ε ( ρ 1 + ρ 2 ) / ℏ μι Εγώ ε ( ρ ένα 1 + ρ σι 2 + ρ ένα 2 + ρ σι 1 ) / 2 ℏ ( ρ 1 ρ 2 ) 1 / 2 μι - ε 2 ( ( σ 1 αμαρτία θ 1 ) 2 + ( σ 2 αμαρτία θ 2 ) 2 ) / 2 ℏ 2 συν [ ε ( ρε 2 αμαρτία θ 2 - ρε 1 αμαρτία θ 1 ) / 2 ℏ + δ ] (5) όπου και είναι σταθερά αναλογικότητας. Επομένως, η πιθανότητα ανίχνευσης σύμπτωσης των φωτονίων είναι δ = ε ( ρ ένα 1 + ρ σι 2 - ρ ένα 2 - ρ σι 1 ) / 2 ℏ ντο ν Π 12 = | ΕΝΑ 12 | 2 Π 12 = | ντο ν | 2 ρ 1 ρ 2 μι - ε 2 ( ( σ 1 αμαρτία θ 1 ) 2 + ( σ 2 αμαρτία θ 2 ) 2 ) / ℏ 2 συν 2 [ ε ( ρε 2 αμαρτία θ 2 - ρε 1 αμαρτία θ 1 ) / 2 ℏ + δ ] (6) Η πιθανότητα της σύμπτωσης ανίχνευσης των φωτονίων είναι ένα προϊόν δύο συναρτήσεων, όπου οι εκθετικές συναρτήσεις αντιστοιχούν σε μια περίθλαση ενός φωτονίου ενός φωτονίου από μονές σχισμές και μια λειτουργία συνημίτου αντιστοιχεί σε παρεμβολές δύο φωτονίων από τη διπλή σχισμή. Δεδομένου ότι τα φωτόνια εμπλέκονται στις διαδρομές μέσω των σχισμών, επομένως, Εξ. 6δεν μπορεί να γραφτεί ως προϊόν δύο ξεχωριστών συναρτήσεων μεταβλητών του φωτονίου 1 και του φωτονίου 2, αντίστοιχα. Εάν καταγράφονται μόνο οι μεμονωμένες θέσεις ανίχνευσης φωτονίων σε κάθε οθόνη χωρίς να υπάρχει συσχετισμός μεταξύ τους, τότε δεν σχηματίζεται μοτίβο παρεμβολών. Μια μεμονωμένη παρεμβολή φωτονίου καταστέλλεται λόγω της κβαντικής εμπλοκής των διαδρομών των φωτονίων στη διπλή σχισμή. Και τα δύο φωτόνια μπορούν να ανιχνευθούν οπουδήποτε τυχαία στις αντίστοιχες οθόνες, ωστόσο, ένα κβαντικό σχέδιο παρεμβολών δύο φωτονίων εμφανίζεται μόνο στις μετρήσεις που σχετίζονται με τη θέση. Η πιθανότητα ανίχνευσης ενός μεμονωμένου φωτονίου στις αντίστοιχες οθόνες μπορεί να υπολογιστεί ενσωματώνοντας όλες τις πιθανές διαδρομές ενός μεμονωμένου φωτονίου. Ωστόσο, Λόγω της κβαντικής εμπλοκής των διαδρομών, αυτό το ακέραιο αποτέλεσμα οδηγεί σε προσθήκη πιθανότητας ανίχνευσης ενός μόνο φωτονίου μέσω κάθε σχισμής διπλής σχισμής. Επομένως, οι πιθανότητες Π 1 και για να βρείτε ένα μόνο φωτόνιο στην οθόνη 1 και στην οθόνη 2 είναι Π 2 Π 1 ∝ 1 ρ 1 μι - ε 2 ( σ 1 αμαρτία θ 1 ) 2 / ℏ 2 (7α) Π 2 ∝ 1 ρ 2 μι - ε 2 ( σ 2 αμαρτία θ 2 ) 2 / ℏ 2 (7β) όπου κάθε κατανομή πιθανότητας μιας ανίχνευσης ενός φωτονίου είναι gaussian και δεν εμφανίζεται ένα μοτίβο παρεμβολής με ένα φωτονίο. Το πραγματικό πείραμα εκτελείται στον τρισδιάστατο χώρο θέσης, όπου η ορμή των φωτονίων και οι αποστάσεις των ανιχνευτών από διπλές σχισμές μετρούνται στον τρισδιάστατο χώρο θέσης. Επομένως, η προβολή της ορμής και των αποστάσεων στο εγκάρσιο επίπεδο θα πρέπει να λαμβάνεται υπόψη ώστε να είναι συνεπής με τις εξισώσεις. 6 και 7 . Στο πραγματικό πείραμα οι σχισμές βρίσκονται παράλληλα με το εγκάρσιο επίπεδο, η μετατόπιση του ανιχνευτή είναι παράλληλη με το εγκάρσιο επίπεδο και το εύρος μετατόπισης είναι τέτοιο ώστε , επομένως, και ε 1 ≪ μικρό 1 ε 2 ≪ μικρό 2 αμαρτία θ 1 ∼ ε 1 / μικρό 1 αμαρτία θ 2 ∼ ε 2 / μικρό 2 . Υπό αυτές τις εκτιμήσεις, οι όροι με τη μορφή αναλογίας, εγκάρσιας ορμής και απόστασης οθόνης από αντίστοιχη διπλή σχισμή, εμφανίζονται στα Εξ. 6 και 7 . Επομένως, η ορμή των φωτονίων και οι αποστάσεις των ανιχνευτών από διπλές σχισμές που μετρώνται στον τρισδιάστατο χώρο θέσης μπορούν να τοποθετηθούν σε αυτές τις εξισώσεις για τον υπολογισμό των σχεδίων. Πείραμα Το πείραμα διπλής σχισμής που παρουσιάζεται σε αυτό το έγγραφο εκτελείται με φωτονικά εμπλεγμένα με ορμή που παράγονται από εκφυλισμένο μη-γραμμικό SPDC 21 , 24 , 39 , 42 , 43 , 44 , 45 , 47 . Ο κρύσταλλος BBO αντλείται από μια εξαιρετική γραμμικά πολωμένη ακτίνα λέιζερ μήκους κύματος 405 nm και κάτω ζεύγη φωτονίων μήκους κύματος 810 nm με συνηθισμένη πόλωση παράγονται κατά την εμπρόσθια κατεύθυνση σε σχήμα κωνικής εκπομπής σύμφωνα με την ορμή και την εξοικονόμηση ενέργειας όπως φαίνεται στο Σχ. 2. Για να δημιουργήσετε μια εικονική διαμόρφωση διπλής σχισμής, δύο διπρισμοί Fresnel τοποθετούνται στη διαδρομή των φωτονίων και τα φωτόνια ανιχνεύονται από φωτοανιχνευτές χιονοστιβάδας με ένα φωτονίο και ρε 1 ρε 2 . Τα οπτικά φίλτρα στενής ζώνης τοποθετούνται μπροστά από κάθε ανιχνευτή φωτονίων για να σταματήσει το φως του φόντου. Τα φωτόνια που έχουν μετατραπεί κάτω έχουν την ίδια συχνότητα και γραμμική πόλωση, η οποία είναι κάθετη με την πόλωση της δέσμης λέιζερ της αντλίας. Η ένταση του λέιζερ της αντλίας είναι τέτοια που η πιθανότητα παραγωγής περισσότερων από ένα ζεύγος φωτονίων είναι εξαιρετικά μικρή. Ο αριθμός των μετρήσεων φωτονίων κάθε ανιχνευτή φωτονίων και οι μετρήσεις αμοιβαίας σύμπτωσής τους μετρώνται με μια μονάδα μέτρησης δύο καναλιών μονής φωτονίας. Η επέκταση εγκάρσιου τρόπου λειτουργίας της δέσμης λέιζερ της αντλίας μειώνεται για να διατηρηθεί το μέγεθος της πηγής πολύ μικρότερο από το διαχωρισμό των σχισμών, αλλά είναι μεγάλο έτσι ώστε να διατηρείται η ορμή εμπλοκής των φωτονίωνΣχήμα 
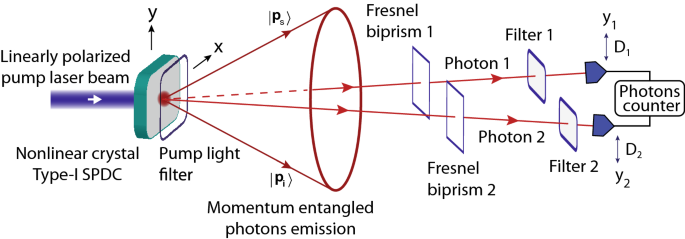
Ένα σχηματικό διάγραμμα της πειραματικής διαμόρφωσης του πειράματος double-double-slit. Τα ζεύγη φωτονίων που εμπλέκονται σε ορμή παράγονται σε κωνικό μοτίβο εκπομπών από μη γραμμικό κρύσταλλο. Μια διαμόρφωση διπλής σχισμής πραγματοποιείται με δύο διμερισμούς FresnelΣχήμα 
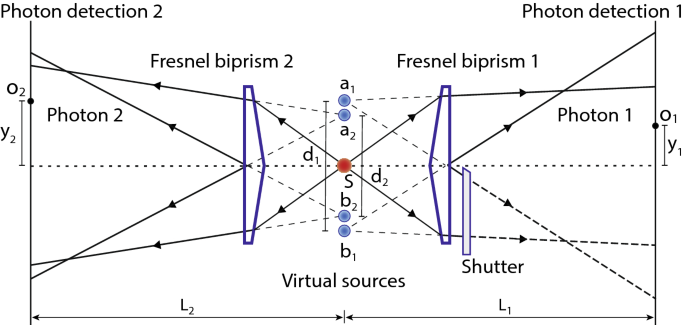
Ένα ξεδιπλωμένο διάγραμμα του πειράματος double-double-slit που πραγματοποιήθηκε με διπρισμούς Fresnel. Οι εικονικές πηγές αντιστοιχούν σε εικονικές σχισμές. Για να ανιχνεύσει ποια διαδρομή διαδρομής των φωτονίων, ένα κλείστρο μπορεί να τοποθετηθεί σε μια διαδρομή του φωτονίου 1 με τέτοιο τρόπο ώστε να αποκλείεται μια εικονική σχισμή . σι 1