Τα κυκλώματα διασταύρωσης Quantum Josephson και η αυγή των τεχνητών ατόμων

Το 1985, τα πειράματα αποκάλυψαν την κβαντική συμπεριφορά ενός μακροσκοπικού βαθμού ελευθερίας: τη διαφορά φάσης σε μια διασταύρωση Josephson. Οι συγγραφείς αναδεικνύουν το ιστορικό αυτού του ορόσημου για την ανάπτυξη υπεραγώγιμων κβαντικών κυκλωμάτων .          Οι μακροσκοπικοί βαθμοί ελευθερίας ακολουθούν την κβαντική μηχανική; Κατά τις πρώτες έξι δεκαετίες της κβαντικής μηχανικής η απάντηση σε αυτή την ερώτηση δεν εξετάστηκε ποτέ πειραματικά. Η κβαντομηχανική ήταν γνωστό ότι επιβιώνει σε μακροσκοπικό επίπεδο μόνο μέσω συλλογικών φαινομένων όπως η υπερρευστότητα, η υπεραγωγιμότητα, η κβαντοποίηση ροής και το φαινόμενο Josephson. Παρόλο που τα φαινόμενα αυτά χαρακτηρίζονται συμβατικά ως «μακροσκοπικά», είναι στην πραγματικότητα κλασσικές εκδηλώσεις σε μακροσκοπική κλίμακα του συνδυασμού μεγάλου αριθμού μικροσκοπικών μεταβλητών, καθένας από τους οποίους διέπεται από την κβαντική μηχανική. Η επικάλυψη ορισμένων κρυστάλλων, όπως ο χαλαζίας, που αποκαλύπτει τους ομοιοπολικούς δεσμούς μεταξύ των συστατικών, αντιπροσωπεύει ένα στοιχειώδες παράδειγμα αυτής της κατηγορίας κβαντικών φαινομένων που παρουσιάζονται σε μακροσκοπική κλίμακαο 1980, ο Anthony Leggett 1 υπογράμμισε τη σημασία της διάκρισης των μακροσκοπικών κβαντικών φαινομένων που προέρχονται από την κάπως ασήμαντη μαζική συσσώρευση των αποτελεσμάτων που προέρχονται από το επίπεδο των μικροσκοπικών μεταβλητών από αυτές που εμφανίζονται, υποθετικά, από έναν ενιαίο μακροσκοπικό, συλλογικό βαθμό ελευθερίας. Παρόλο που τίποτα θεωρητικά δεν φαίνεται να εμποδίζει τέτοιες μεταβλητές από την πλήρη υπακοή στην κβαντομηχανική, αισθανόμασταν πρόκληση να διαπιστώσουμε αν πράγματι συνέβαινε στην πράξη.

Το 1985, απαντήσαμε στην ερώτηση με την πειραματική μας παρατήρηση 2 των κβαντισμένων ενεργειακών επιπέδων μιας τρέχουσας μεροληψίας κόμβου Josephson 3 , 4 . Βασικά, οι μετρούμενες τιμές των ενεργειακών επιπέδων συμφωνήθηκαν ποσοτικά με κβαντομηχανικές προβλέψεις με βάση παραμέτρους της διασταύρωσης που είχαμε μετρήσει κλασικά, in situ 5 .

Η διασταύρωση της σήραγγας Josephson αποτελείται από δύο υπεραγωγούς που χωρίζονται από ένα λεπτό μονωτικό φράγμα διαμέσου του οποίου τα ζευγάρια των ηλεκτρονίων Cooper μπορούν να τούνουν συνεκτικά. Για κάθε υπεραγωγό, η πυκνότητα των ζευγών Cooper και η κοινή τους φάση περιγράφουν την μακροσκοπική κβαντική κατάσταση. Στη δεκαετία του 1980, οι διασταυρώσεις Josephson χρησιμοποιήθηκαν μόνο σε κλασικές υπεραγωγικές ηλεκτρονικές συσκευές, για παράδειγμα υπεραγωγικές συσκευές κβαντικής παρεμβολής (SQUID) 6 και το πρότυπο βολτ 7 .

Στο πείραμά μας ερευνήσαμε τη συμπεριφορά μίας μόνο μακροσκοπικής μεταβλητής - η διαφορά φάσης δ μεταξύ των δύο υπεραγωγών που μετράται όταν υπάρχει μηδενική στατική τάση στο φράγμα. Παρόλο που η διαφορά φάσης ονόματος μπορεί να υποδηλώνει μια de facto κβαντομηχανική μεταβλητή, αυτό δεν συμβαίνει. Στην ουσία, μπορεί κανείς να κατανοήσει τη διαφορά φάσης ως ένα είδος ορμής του κέντρου της μάζας των ζευγαριών Cooper καθώς ρέουν σε μια διασταύρωση. Είναι μια συλλογική μεταβλητή που συνδέεται με όλα τα ηλεκτρόνια της διασταύρωσης, όπως το φορτίο στα ηλεκτρόδια ενός πυκνωτή.

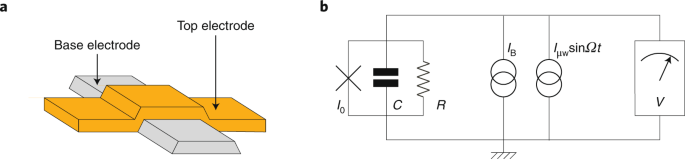
Για τα πειράματα μας, έχουμε μοτίβο Nb-NbO x -PbIn διασταυρώσεις τούνελ photolithograhically σε οξειδωμένη μάρκες Si σε είτε ένα 10 × 10 μm 2 ή 80 × 10 μm 2 γεωμετρία εγκάρσιας λωρίδας (Εικ. 1a ). Για να γίνει η μέτρηση, όπως φαίνεται στην Εικόνα 1b , συζεύξαμε κάθε κόμβο με τη σειρά του σε μία στατική πηγή ρεύματος και μια πηγή μικροκυμάτων στη συχνότητα Ω / 2π και χρησιμοποιήσαμε έναν ενισχυτή χαμηλού θορύβου για να ανιχνεύσουμε οποιαδήποτε τάση V που αναπτύχθηκε. Η διασταύρωση απομακρύνεται από μια χωρητικότητα C , η οποία κυριαρχείται από την εγγενή χωρητικότητα σύνδεσης και μια αντίσταση R , η οποία κυριαρχείται από τις συνεισφορές από το εξωτερικό κύκλωμαΕικόνα 1: Η διασταύρωση Josephson και το κύκλωμα μέτρησης.

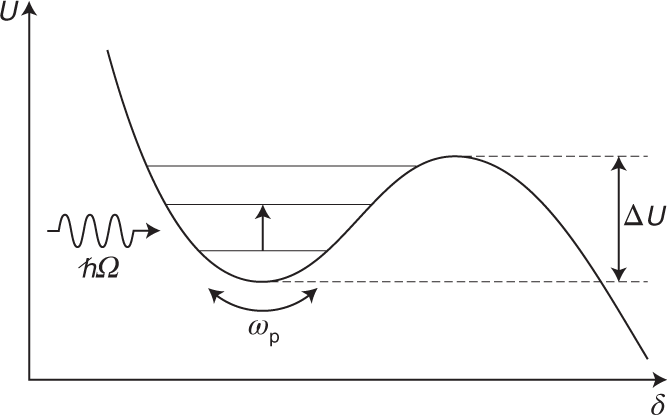
α , Σχηματική διασταύρωση σήραγγας διασταυρωμένης λωρίδας Josephson. Οι συσκευές μας αποτελούνται από ένα ηλεκτρόδιο βάσης Nb και ένα κορυφαίο ηλεκτρόδιο κράματος PbIn που διαχωρίζεται από μια στιβάδα Nb-οξειδίου πυκνότητας ~ 1 nm που σχηματίζεται από οξείδωση πλάσματος του ηλεκτροδίου βάσης. β , σχηματική παράσταση ενός στοιχείου Josephson (σταυροειδής) που απομακρύνεται από μια χωρητικότητα C και αντίσταση R , και συνδέεται στις πηγές ρεύματος στατικής πόλωσης ( I B ) και μικροκυμάτων ( I μw ). Η τάση V κατά μήκος της διασταύρωσης μετριέται από μια αλυσίδα ενισχυτή χαμηλής έντασης ήχου που αντιπροσωπεύεται συμβολικά. Ο πίνακας b προσαρμόζεται με την άδεια από τον αναφ. 2 , APS.Εικόνα 2: Κυβικό δυναμικό στο οποίο η μακροσκοπική διαφορά φάσης δ της διακλάδωσης εξελίσσεται κβαντικά μηχανικά.

Η ακτινοβολία μικροκυμάτων στη συχνότητα Ω / 2π επάγει μεταβάσεις μεταξύ των επιπέδων ενέργειας που προβλέπει η κβαντική μηχανική στο φρεάτιο. Αυτές οι μεταβάσεις ανιχνεύονται με ενίσχυση της ταχύτητας σήραγγας, μετρούμενη στη διαμόρφωση του σχήματος 1 b . Οι συχνότητες μετάβασης είναι συγκρίσιμες με τη συχνότητα πλάσματος ω p / 2π. Σχήμα προσαρμοσμένο με άδεια από τον αναφ. 5 , APS. /div>
Η κβαντομηχανική προβλέπει ότι η ενέργεια του σωματιδίου στο φρεάτιο είναι κβαντισμένη, όπως υποδεικνύεται στο σχήμα 2 . Ο 3/2 εκθέτης στο ΔU συνδέεται με ένα δυναμικό κυβικού σχήματος, το οποίο οδηγεί σε μείωση της απόστασης των ενεργειακών επιπέδων στο φρεάτιο με την αύξηση της ενέργειας, όπως στο άτομο του υδρογόνου. Η αύξηση του ρεύματος πόλωσης Ι μειώνει επίσης την απόσταση όλων των επιπέδων ενέργειας. Όπως θα δούμε, είναι κεντρικής σημασίας ότι το καλοκαίρι να είναι ανόμονο. Το τετραγωνικό δυναμικό ενός απλού αρμονικού ταλαντωτή οδηγεί σε απόσταση μεταξύ των επιπέδων ενέργειας που είναι ανεξάρτητη από τον αριθμό στάθμης για όλους τους κβαντικούς αριθμούς. Αντίθετα, οι μεταβάσεις μεταξύ των επιπέδων ενός ανόρμικου φρεατίου με μικρούς κβαντικούς αριθμούς μπορούν να επιλυθούν απλά, σε αντίθεση με τους μεγάλους κβαντικούς αριθμούς όπου η αρχή αλληλογραφίας του Bohr πρέπει πάντα να διατηρεί. Όπως έχει υπογραμμίσει το Leggett 1 τόσο εύγλωττα, η χρήση ενός ανιχνευτικού ταλαντωτή επιτρέπει σε κάποιον να «αποφύγει το όριο αλληλογραφίας». Το σωματίδιο μπορεί να διαφύγει από το πηγάδι με δύο διαδικασίες. Στο κλασικό όριο k B T / ħω p » 1 / 2π το σωματίδιο διαφεύγει με θερμικό θόρυβο που τον ενεργοποιεί πάνω από το φράγμα. εδώ k B είναι η σταθερά Boltzmann, T είναι η θερμοκρασία και ħ ≡ h / 2π. Σε αυτή την περίπτωση, δ δρα ως κλασσική μεταβλητή. Στο κβαντικό όριο k B T / ħω p " 1 / 2π, από την άλλη πλευρά, το σωματίδιο συμπεριφέρεται ως πακέτο κύματος και η διαφορά φάσης δενεργεί ως κβαντικός φορέας εκμετάλλευσης και όχι ως κλασικός αριθμός. Δεδομένου ότι η ουρά του πακέτου κυμάτων εκτείνεται κάτω από το φράγμα, το σωματίδιο μπορεί να διαφύγει με μακροσκοπική κβαντική σήραγγα μέσω του φραγμού 11 , 12 , 13 , 14 . Για να επιβεβαιώσουμε την παρουσία κβαντοποιημένων επιπέδων ενέργειας στη διασταύρωση στο κβαντικό καθεστώς, στοχεύσαμε στη μέτρηση της αύξησης του ρυθμού σήραγγας μετά από μεταβάσεις μεταξύ των επιπέδων ενέργειας που προκαλούνται από την ακτινοβολία μικροκυμάτων. Για να συγκρίνουμε τα πειραματικά μας αποτελέσματα με τις θεωρητικές προβλέψεις, χρησιμοποιήσαμε πρώτα την ενεργοποίηση συντονισμού 15 για να μετρήσουμε τις κλασικές ιδιότητες κάθε κόμβου μας με την ίδια ακολουθία ψύξης. Όταν ένας κόμβος είναι ρεύμα-προκατειλημμένη παρακάτω Ι 0 σε κατάσταση μηδενικής τάσεως του με το σωματίδιο εντοπίζεται σε ένα φρέαρ δυναμικού, θερμικές διακυμάνσεις ρυθμίζουν τη γωνία της κλίσης της σανίδα μπουγάδας και να προκαλέσει το σωματίδιο να ενεργοποιηθεί έξω από το πηγάδι. Για μια ένωση με υποπίεση, η οποία έχει χαρακτηριστικό υστερετικής τάσης ρεύματος, το σωματίδιο τρέχει κάτω από το πινάκιο, δημιουργώντας τάση στην διασταύρωση. Η βασική ιδέα της συντονισμένης ενεργοποίησης είναι η εφαρμογή μικροκυμάτων με ισχύ P σε συχνότητα Ω/ 2π σε ή κοντά στη συχνότητα πλάσματος, η οποία είναι συνήθως αρκετά GHz, στη διασταύρωση στο κλασικό (θερμικό) καθεστώς. Αυτό προσθέτει μια μικρή διαταραχή στη δυναμική του σωματιδίου παρουσία θερμικού θορύβου, αυξάνοντας την ταχύτητα ενεργοποίησης του σωματιδίου από το φρεάτιο και μειώνοντας έτσι τη διάρκεια ζωής του τ . Μέσα σε λίγες μέρες από τη σύλληψη αυτής της ιδέας, επαληθεύσαμε το βασικό φαινόμενο με έναν αναλογικό υπολογιστή προγραμματισμένο να προσομοιώνει μια διασταύρωση Josephson. Μαζί με τον Daniel Esteve, πραγματοποιήσαμε προσομοιώσεις ηλεκτρονικών υπολογιστών για να δείξουμε με περισσότερες λεπτομέρειες πώς θα μπορούσαμε να εξαγάγουμε παραμέτρους από αυτόν τον συντονισμό. Μετρήσαμε τ σε 4.2 Κ ως συνάρτηση του Ι , Ρ και Ω ? Q και I 0 προέκυψαν από διαφορετικά χαρακτηριστικά της κορυφής θερμικής ενεργοποίησης. Για να εξαγάγουμε επακριβώς αυτές τις παραμέτρους από τα δεδομένα, πραγματοποιήσαμε αρχικά μια αριθμητική προσομοίωση της διασταύρωσης παρουσία θερμικού θορύβου. Από τις μετρήσεις και τις προσομοιώσεις της διασταύρωσης παρουσία θερμικού θορύβου εξάγουμε ω p και συνεπώς ω p0 και C , τότε R = Q / ω p C- που μας επιτρέπουν να κάνουμε ακριβείς μετρήσεις όλων των σχετικών παραμέτρων στο κλασικό καθεστώς. Περαιτέρω θεωρητικές αναλύσεις 16 , 17 επιβεβαίωσαν αργότερα τις προσομοιώσεις μας. Αφού αποκτήσαμε τις τιμές των παραμέτρων διασταύρωσης και του κυκλώματος, βρισκόμασταν τότε σε θέση να μετρήσουμε τα ποσοτικά επίπεδα ενέργειας και να συγκρίνουμε τις τιμές τους με τις θεωρητικές προβλέψεις χωρίς να έχουμε προσαρμοσμένες παραμέτρους. Κάναμε τις μετρήσεις στο κβαντικό όριο σε θερμοκρασίες μερικών δεκάδων millikelvin. Η βάση του πειράματος ήταν η μέτρηση της μεταβολής του ρυθμού διαφυγής Γ ( Ρ ) - Γ (0) της διακλάδωσης από το καθεστώς μηδενικής τάσης ως συνάρτηση του ρεύματος προκατάμεσης Ι . Καθορίσαμε το Γ (0) και το Γ ( Ρ ) ξεχωριστά, αυξάνοντας επανειλημμένα το ρεύμα προκατάμενου για να λάβουμε ένα ιστόγραμμα του ρεύματος στο οποίο η διασταύρωση μετατράπηκε στην κατάσταση τάσης. Υπολογίσαμε τους ρυθμούς διαφυγής από τα ιστογράμματα και στη συνέχεια υπολογίσαμε τα Γ ( P ) - Γ (0). Συνήθως, υπολογίσαμε κατά μέσον όρο πάνω από 10 5 συμβάντα αλλαγής. Διαφέραμε Γ (0) από 10 2 έως 105 s -1 και ρυθμίσαμε την ισχύ μικροκυμάτων P για παραγωγή [ Γ ( Ρ ) - Γ (0)] / Γ (0)